Advertisements
Advertisements
Question
A metal cube of length 4 cm radiates heat at the rate of 10 J/s. Find its emissive power at a given temperature.
Solution
Given: l = 4 cm, A = 6l2 = 6 × 16 cm2 = 96 × 10-4 m2
`Q/t = 10` J/s
To find: Emissive power (E)
Formula:
E = `Q/(At)`
Calculation:
From formula,
E = `10/(96 xx 10^-4)`
= 1041.66 J/m2s
The emissive power at a given temperature is 1041.66 J/m2s.
RELATED QUESTIONS
When we place a gas cylinder on a van and the van moves, does the kinetic energy of the molecules increase? Does the temperature increase?
A gas is kept in an enclosure. The pressure of the gas is reduced by pumping out some gas. Will the temperature of the gas decrease by Charles's low?
Is it possible to boil water at room temperature, say 30°C? If we touch a flask containing water boiling at this temperature, will it be hot?
When you come out of a river after a dip, you feel cold. Explain.
A gas cylinder has walls that can bear a maximum pressure of 1.0 × 106 Pa. It contains a gas at 8.0 × 105 Pa and 300 K. The cylinder is steadily heated. Neglecting any change in the volume, calculate the temperature at which the cylinder will break.
The temperature and pressure at Simla are 15.0°C and 72.0 cm of mercury and at Kalka these are 35.0°C and 76.0 cm of mercury. Find the ratio of air density at Kalka to the air density at Simla.
Use R=8.314J K-1 mol-1
The mean speed of the molecules of a hydrogen sample equals the mean speed of the molecules of a helium sample. Calculate the ratio of the temperature of the hydrogen sample to the temperature of the helium sample.
Use R = 8.314 JK-1 mol-1
One mole of an ideal gas undergoes a process `P = (P_0)/(1+(V/V_0)^2` where `p_0` and `V_0` are constants . Find the temperature of the gas when `V=V_0` .
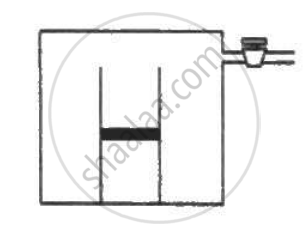
An ideal gas is kept in a long cylindrical vessel fitted with a frictionless piston of cross-sectional area 10 cm2 and weight 1 kg in figure. The vessel itself is kept in a big chamber containing air at atmospheric pressure 100 kPa. The length of the gas column is 20 cm. If the chamber is now completely evacuated by an exhaust pump, what will be the length of the gas column? Assume the temperature to remain constant throughout the process.
An adiabatic cylindrical tube of cross-sectional area 1 cm2 is closed at one end and fitted with a piston at the other end. The tube contains 0.03 g of an ideal gas. At 1 atm pressure and at the temperature of the surrounding, the length of the gas column is 40 cm. The piston is suddenly pulled out to double the length of the column. The pressure of the gas falls to 0.355 atm. Find the speed of sound in the gas at atmospheric temperature.
When a gas is heated, its temperature increases. Explain this phenomenon on the basis of the kinetic theory of gases.
Find the kinetic energy of 5 litres of a gas at STP, given the standard pressure is 1.013 × 105 N/m2.
Compare the rates of emission of heat by a blackbody maintained at 727°C and at 227°C, if the black bodies are surrounded by an enclosure (black) at 27°C. What would be the ratio of their rates of loss of heat?
Earth’s mean temperature can be assumed to be 280 K. How will the curve of blackbody radiation look like for this temperature? Find out λmax. In which part of the electromagnetic spectrum, does this value lie? (Take Wien's constant b = 2.897 × 10−3 m K)
Calculate the energy radiated in one minute by a blackbody of surface area 200 cm2 at 127 °C (σ = 5.7 x 10-8 J m-2 s-1 K-4)
Above what temperature, all bodies radiate electromagnetic radiation?
Compare the rate of radiation of metal bodies at 727 °C and 227 °C.
The average translational kinetic energy of gas molecules depends on ____________.
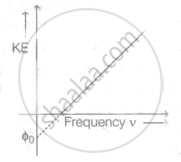
The graph of kinetic energy against the frequency v of incident light is as shown in the figure. The slope of the graph and intercept on X-axis respectively are ______.
Average kinetic energy of H2 molecule at 300K is 'E'. At the same temperature, average kinetic energy of O2 molecule will be ______.
The average translational kinetic energy of a molecule in a gas is 'E1'. The kinetic energy of the electron (e) accelerated from rest through p.d. 'V' volt is 'E2'. The temperature at which E1 = E2 is possible, is ______.
An ideal gas in a container of volume 500 cc is at a pressure of 2 × 105 N/m2. The average kinetic energy of each molecule is 6 × 10−21 J. The number of gas molecules in the container is ______.
Consider a rectangular block of wood moving with a velocity v0 in a gas at temperature T and mass density ρ. Assume the velocity is along x-axis and the area of cross-section of the block perpendicular to v0 is A. Show that the drag force on the block is `4ρAv_0 sqrt((KT)/m)`, where m is the mass of the gas molecule.
23Ne decays to 23Na by negative beta emission. Mass of 23Ne is 22.994465 amu mass of 23Na is 22.989768 amu. The maximum kinetic energy of emitted electrons neglecting the kinetic energy of recoiling product nucleus is ______ MeV.
The Q-value of a nuclear reaction and kinetic energy of the projectile particle, KP are related as ______.
Assuming the expression for the pressure P exerted by an ideal gas, prove that the kinetic energy per unit volume of the gas is `3/2` P.
If a = 0. 72 and r = 0.24, then the value of t is ______.
