Advertisements
Advertisements
Question
Write the coordinates of the orthocentre of the triangle formed by points (8, 0), (4, 6) and (0, 0).
Solution
The intersection point of three altitudes of a triangle is called orthocentre.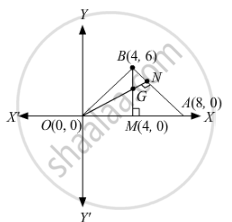
In the figure, two altitudes ON and BM of ∆OAB are shown.
Slope of AB = \[\frac{6 - 0}{4 - 8} = - \frac{3}{2}\]
\[\therefore\] Slope of ON \[= \frac{2}{3} \left( \because \text{ Product of slopes }= - 1 \right)\]
Equation of ON:
\[\left( y - 0 \right) = \frac{2}{3}\left( x - 0 \right)\]
\[y = \frac{2}{3}x\] ... (1)
Equation of BM:
x = 4 ... (2)
On solving equations (1) and (2), we get
APPEARS IN
RELATED QUESTIONS
If the line segment joining the points P (x1, y1) and Q (x2, y2) subtends an angle α at the origin O, prove that
OP · OQ cos α = x1 x2 + y1, y2
Four points A (6, 3), B (−3, 5), C (4, −2) and D (x, 3x) are given in such a way that \[\frac{\Delta DBC}{\Delta ABC} = \frac{1}{2}\]. Find x.
The points A (2, 0), B (9, 1), C (11, 6) and D (4, 4) are the vertices of a quadrilateral ABCD. Determine whether ABCD is a rhombus or not.
Find the coordinates of the centre of the circle inscribed in a triangle whose vertices are (−36, 7), (20, 7) and (0, −8).
The base of an equilateral triangle with side 2a lies along the y-axis, such that the mid-point of the base is at the origin. Find the vertices of the triangle.
Find the distance between P (x1, y1) and Q (x2, y2) when (i) PQ is parallel to the y-axis (ii) PQ is parallel to the x-axis.
Find the locus of a point equidistant from the point (2, 4) and the y-axis.
Find the equation of the locus of a point which moves such that the ratio of its distances from (2, 0) and (1, 3) is 5 : 4.
Find the locus of a point such that the sum of its distances from (0, 2) and (0, −2) is 6.
Find the locus of a point which is equidistant from (1, 3) and the x-axis.
Find the locus of a point which moves such that its distance from the origin is three times its distance from the x-axis.
A (5, 3), B (3, −2) are two fixed points; find the equation to the locus of a point P which moves so that the area of the triangle PAB is 9 units.
If A (−1, 1) and B (2, 3) are two fixed points, find the locus of a point P, so that the area of ∆PAB = 8 sq. units.
Find the locus of the mid-point of the portion of the line x cos α + y sin α = p which is intercepted between the axes.
If O is the origin and Q is a variable point on y2 = x, find the locus of the mid-point of OQ.
What does the equation (x − a)2 + (y − b)2 = r2 become when the axes are transferred to parallel axes through the point (a − c, b)?
What does the equation (a − b) (x2 + y2) −2abx = 0 become if the origin is shifted to the point \[\left( \frac{ab}{a - b}, 0 \right)\] without rotation?
Find what the following equation become when the origin is shifted to the point (1, 1).
xy − y2 − x + y = 0
To what point should the origin be shifted so that the equation x2 + xy − 3x − y + 2 = 0 does not contain any first degree term and constant term?
Find what the following equation become when the origin is shifted to the point (1, 1).
xy − y2 − x + y = 0
Find what the following equation become when the origin is shifted to the point (1, 1).
xy − x − y + 1 = 0
Find what the following equation become when the origin is shifted to the point (1, 1).
x2 − y2 − 2x + 2y = 0
Find the point to which the origin should be shifted after a translation of axes so that the following equation will have no first degree terms: y2 + x2 − 4x − 8y + 3 = 0
Find the point to which the origin should be shifted after a translation of axes so that the following equation will have no first degree terms: x2 + y2 − 5x + 2y − 5 = 0
Find the point to which the origin should be shifted after a translation of axes so that the following equation will have no first degree terms: x2 − 12x + 4 = 0
Verify that the area of the triangle with vertices (4, 6), (7, 10) and (1, −2) remains invariant under the translation of axes when the origin is shifted to the point (−2, 1).
In Q.No. 1, write the distance between the circumcentre and orthocentre of ∆OAB.
Three vertices of a parallelogram, taken in order, are (−1, −6), (2, −5) and (7, 2). Write the coordinates of its fourth vertex.
If the points (a, 0), (at12, 2at1) and (at22, 2at2) are collinear, write the value of t1 t2.
Write the coordinates of the in-centre of the triangle with vertices at (0, 0), (5, 0) and (0, 12).
If the points (1, −1), (2, −1) and (4, −3) are the mid-points of the sides of a triangle, then write the coordinates of its centroid.
