Advertisements
Advertisements
Question
The base of an equilateral triangle with side 2a lies along the y-axis, such that the mid-point of the base is at the origin. Find the vertices of the triangle.
Solution
Let ABC be an equilateral triangle, where BC = 2a. Let A(x, 0) be the third vertex of \[∆\] ABC.
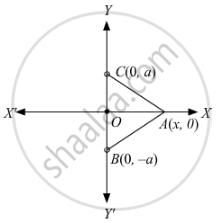
AB = BC = AC \[\Rightarrow\] \[{AB}^2 {= BC}^2 {= AC}^2\]
\[\Rightarrow a^2 + x^2 = \left( 2a \right)^2 \left( \because BC = 2a \right)\]
\[ \Rightarrow x^2 = 3 a^2 \]
\[ \Rightarrow x = \pm \sqrt{3}a\]
So, the vertices of the triangle are
APPEARS IN
RELATED QUESTIONS
If the line segment joining the points P (x1, y1) and Q (x2, y2) subtends an angle α at the origin O, prove that
OP · OQ cos α = x1 x2 + y1, y2
Four points A (6, 3), B (−3, 5), C (4, −2) and D (x, 3x) are given in such a way that \[\frac{\Delta DBC}{\Delta ABC} = \frac{1}{2}\]. Find x.
The points A (2, 0), B (9, 1), C (11, 6) and D (4, 4) are the vertices of a quadrilateral ABCD. Determine whether ABCD is a rhombus or not.
Find the coordinates of the centre of the circle inscribed in a triangle whose vertices are (−36, 7), (20, 7) and (0, −8).
Find the distance between P (x1, y1) and Q (x2, y2) when (i) PQ is parallel to the y-axis (ii) PQ is parallel to the x-axis.
Find the locus of a point equidistant from the point (2, 4) and the y-axis.
Find the equation of the locus of a point which moves such that the ratio of its distances from (2, 0) and (1, 3) is 5 : 4.
Find the locus of a point which is equidistant from (1, 3) and the x-axis.
Find the locus of a point which moves such that its distance from the origin is three times its distance from the x-axis.
A (5, 3), B (3, −2) are two fixed points; find the equation to the locus of a point P which moves so that the area of the triangle PAB is 9 units.
Find the locus of a point such that the line segments with end points (2, 0) and (−2, 0) subtend a right angle at that point.
A rod of length l slides between two perpendicular lines. Find the locus of the point on the rod which divides it in the ratio 1 : 2.
Find the locus of the mid-point of the portion of the line x cos α + y sin α = p which is intercepted between the axes.
If O is the origin and Q is a variable point on y2 = x, find the locus of the mid-point of OQ.
What does the equation (a − b) (x2 + y2) −2abx = 0 become if the origin is shifted to the point \[\left( \frac{ab}{a - b}, 0 \right)\] without rotation?
Find what the following equation become when the origin is shifted to the point (1, 1).
x2 + xy − 3x − y + 2 = 0
Find what the following equation become when the origin is shifted to the point (1, 1).
xy − y2 − x + y = 0
To what point should the origin be shifted so that the equation x2 + xy − 3x − y + 2 = 0 does not contain any first degree term and constant term?
Verify that the area of the triangle with vertices (2, 3), (5, 7) and (− 3 − 1) remains invariant under the translation of axes when the origin is shifted to the point (−1, 3).
Find what the following equation become when the origin is shifted to the point (1, 1).
xy − y2 − x + y = 0
Find what the following equation become when the origin is shifted to the point (1, 1).
x2 − y2 − 2x + 2y = 0
Find the point to which the origin should be shifted after a translation of axes so that the following equation will have no first degree terms: y2 + x2 − 4x − 8y + 3 = 0
Find the point to which the origin should be shifted after a translation of axes so that the following equation will have no first degree terms: x2 − 12x + 4 = 0
The vertices of a triangle are O (0, 0), A (a, 0) and B (0, b). Write the coordinates of its circumcentre.
Three vertices of a parallelogram, taken in order, are (−1, −6), (2, −5) and (7, 2). Write the coordinates of its fourth vertex.
Write the coordinates of the in-centre of the triangle with vertices at (0, 0), (5, 0) and (0, 12).
