Advertisements
Advertisements
Question
Write the number of ways in which 7 men and 7 women can sit on a round table such that no two women sit together ?
Solution
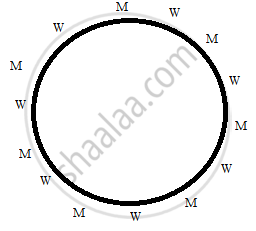
Each of the seven men can be arranged amongst themselves in 7! ways.
The women can be arranged amongst themselves in seven places, in 6! ways (i.e. nthings can be arranged in (n-1)! ways around a round table).
By fundamental principle of counting, total number of ways = 7! x 6!
APPEARS IN
RELATED QUESTIONS
Evaluate 4! – 3!
Is 3! + 4! = 7!?
Find r if `""^5P_r = 2^6 P_(r-1)`
How many words, with or without meaning, can be formed using all the letters of the word EQUATION, using each letter exactly once?
In how many ways can the letters of the word PERMUTATIONS be arranged if the vowels are all together.
In how many ways can the letters of the word ASSASSINATION be arranged so that all the S’s are together?
How many natural numbers not exceeding 4321 can be formed with the digits 1, 2, 3 and 4, if the digits can repeat?
How many three digit numbers can be formed by using the digits 0, 1, 3, 5, 7 while each digit may be repeated any number of times?
Find the number of ways in which 8 distinct toys can be distributed among 5 childrens.
Write the total number of possible outcomes in a throw of 3 dice in which at least one of the dice shows an even number.
Write the number of words that can be formed out of the letters of the word 'COMMITTEE' ?
Write the number of ways in which 6 men and 5 women can dine at a round table if no two women sit together ?
The number of permutations of n different things taking r at a time when 3 particular things are to be included is
The number of ways to arrange the letters of the word CHEESE are
If k + 5Pk + 1 =\[\frac{11 (k - 1)}{2}\]. k + 3Pk , then the values of k are
How many 6-digit telephone numbers can be constructed with the digits 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 if each numbers starts with 35 and no digit appear more than once?
Find the rank of the word ‘CHAT’ in the dictionary.
Evaluate the following.
`(3! xx 0! + 0!)/(2!)`
The total number of 9 digit number which has all different digit is:
Determine the number of permutations of the letters of the word SIMPLE if all are taken at a time?
A test consists of 10 multiple choice questions. In how many ways can the test be answered if the first four questions have three choices and the remaining have five choices?
A student appears in an objective test which contain 5 multiple choice questions. Each question has four choices out of which one correct answer.
What is the maximum number of different answers can the students give?
If the letters of the word GARDEN are permuted in all possible ways and the strings thus formed are arranged in the dictionary order, then find the ranks of the words
GARDEN
Find the number of strings that can be made using all letters of the word THING. If these words are written as in a dictionary, what will be the 85th string?
Choose the correct alternative:
If `""^(("n" + 5))"P"_(("n" + 1)) = ((11("n" - 1))/2)^(("n" + 3))"P"_"n"`, then the value of n are
Suppose m men and n women are to be seated in a row so that no two women sit together. If m > n, show that the number of ways in which they can be seated is `(m!(m + 1)!)/((m - n + 1)1)`
Three married couples are to be seated in a row having six seats in a cinema hall. If spouses are to be seated next to each other, in how many ways can they be seated? Find also the number of ways of their seating if all the ladies sit together.
The number of signals that can be sent by 6 flags of different colours taking one or more at a time is ______.
In a certain city, all telephone numbers have six digits, the first two digits always being 41 or 42 or 46 or 62 or 64. How many telephone numbers have all six digits distinct?
Using the digits 1, 2, 3, 4, 5, 6, 7, a number of 4 different digits is formed. Find
| C1 | C2 |
| (a) How many numbers are formed? | (i) 840 |
| (b) How many number are exactly divisible by 2? | (i) 200 |
| (c) How many numbers are exactly divisible by 25? | (iii) 360 |
| (d) How many of these are exactly divisible by 4? | (iv) 40 |
Let b1, b2, b3, b4 be a 4-element permutation with bi ∈ {1, 2, 3, .......,100} for 1 ≤ i ≤ 4 and bi ≠ bj for i ≠ j, such that either b1, b2, b3 are consecutive integers or b2, b3, b4 are consecutive integers. Then the number of such permutations b1, b2, b3, b4 is equal to ______.
If the letters of the word 'MOTHER' be permuted and all the words so formed (with or without meaning) be listed as in a dictionary, then the position of the word 'MOTHER' is ______.
