Advertisements
Advertisements
Question
यदि द्विघात बहुपद ax2 + bx + c, c ≠ 0 के शून्यक बराबर हैं, तो ______ ।
Options
c और a विपरीत चिन्हों के हैं
c और b विपरीत चिन्हों के है
c और a एक ही चिन्ह के हैं
c और b एक ही चिन्ह के हैं
Solution
यदि द्विघात बहुपद ax2 + bx + c, c ≠ 0 के शून्यक बराबर हैं, तो c और a एक ही चिन्ह के हैं।
स्पष्टीकरण:
दिए गए द्विघात बहुपद ax2 + bx + c जहां c ≠ 0 के शून्यक बराबर हैं।
यदि x2 के गुणांक और स्थिर पद का चिह्न एक ही है यानी c और a का चिह्न समान है।
जबकि b यानी, x का गुणांक धनात्मक या ऋणात्मक हो सकता है लेकिन शून्य नहीं।
विचार करना,
(i) x2 + 4x + 4 = 0
`\implies` (x + 2)2 = 0
`\implies` x = –2, –2
(ii) x2 – 4x + 4 = 0
`\implies` (x – 2)2 = 0
`\implies` x = 2, 2
APPEARS IN
RELATED QUESTIONS
किसी बहुपद p(x) के लिए, y = p(x) का ग्राफ नीचे आकृति में दिया है। निम्नलिखित स्थिति में, p(x) के शून्यकों की संख्या ज्ञात कीजिए।

किसी बहुपद p(x) के लिए, y = p(x) का ग्राफ नीचे आकृति में दिया है। निम्नलिखित स्थिति में, p(x) के शून्यकों की संख्या ज्ञात कीजिए।
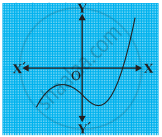
किसी बहुपद p(x) के लिए, y = p(x) का ग्राफ नीचे आकृति में दिया है। निम्नलिखित स्थिति में, p(x) के शून्यकों की संख्या ज्ञात कीजिए।
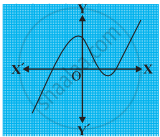
किसी बहुपद p(x) के लिए, y = p(x) का ग्राफ नीचे आकृति में दिया है। निम्नलिखित स्थिति में, p(x) के शून्यकों की संख्या ज्ञात कीजिए।
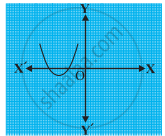
किसी बहुपद p(x) के लिए, y = p(x) का ग्राफ नीचे आकृति में दिया है। निम्नलिखित स्थिति में, p(x) के शून्यकों की संख्या ज्ञात कीजिए।
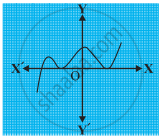
यदि द्विधात बहुपद x2 + (a + 1) x + b के शून्यक 2 और –3 हैं, तो
द्विघात बहुपद् x2 + kx + k, k ≠ 0 के शून्यक ______।
निम्नलिखित में से कौन एक द्विघात बहुपद का आलेख नहीं है?
यदि एक बहुपद का आलेख x-अक्ष को केवल एक ही बिंदु पर प्रतिच्छेद करे, तो यह एक द्विघात बहुपद् नहीं हो सकता।
यद् एक बहुपद का आलेख x-अक्ष को ठीक दो बिन्दुओं पर प्रतिच्छेद करता है, तो यह आवश्यक नहीं है कि वह एक द्विधात बहुपद हो।
