Advertisements
Advertisements
Question
You are given four sources of light each one providing a light of a single colour – red, blue, green and yellow. Suppose the angle of refraction for a beam of yellow light corresponding to a particular angle of incidence at the interface of two media is 90°. Which of the following statements is correct if the source of yellow light is replaced with that of other lights without changing the angle of incidence?
Options
The beam of red light would undergo total internal reflection.
The beam of red light would bend towards normal while it gets refracted through the second medium.
The beam of blue light would undergo total internal reflection.
The beam of green light would bend away from the normal as it gets refracted through the second medium.
Solution
The beam of blue light would undergo total internal reflection.
Explanation:
According to the Cauchy relationship, `lambda oo 1/mu`
Smaller the wavelength higher the refractive index and consequently smaller the critical angle.
We know `v = flambda`, the frequency of wave remains unchanged with medium hence `v oo lambda`.
The critical angle, sin C = `1/mu`
Also, velocity of light, `v oo 1/mu`
According to VIBGYOR, among all given sources of light, the blue light have smallest wavelength, As `lambda_("blu") < lambda_("yellow")` hence `v_("blue") < v_("yellow")`, it means `mu_("blue") > mu_("yellow")`
It means critical angle for blue is less than yellow colour, the critical angle is least which facilitates total internal reflection for the beam of blue light.
APPEARS IN
RELATED QUESTIONS
A small candle, 2.5 cm in size is placed at 27 cm in front of a concave mirror of radius of curvature 36 cm. At what distance from the mirror should a screen be placed in order to obtain a sharp image? Describe the nature and size of the image. If the candle is moved closer to the mirror, how would the screen have to be moved?
A man uses a concave mirror for shaving. He keeps his face at a distance of 25 cm from the mirror and gets an image which is 1.4 times enlarged. Find the focal length of the mirror.
A diverging lens of focal length 20 cm and a converging mirror of focal length 10 cm are placed coaxially at a separation of 5 cm. Where should an object be placed so that a real image is formed at the object itself?
Answer the following question.
Three lenses of focal length +10 cm, —10 cm and +30 cm are arranged coaxially as in the figure given below. Find the position of the final image formed by the combination.

According to Cartesian sign convention, all distances are measured from the _______.
According to the mirror equation, ______.
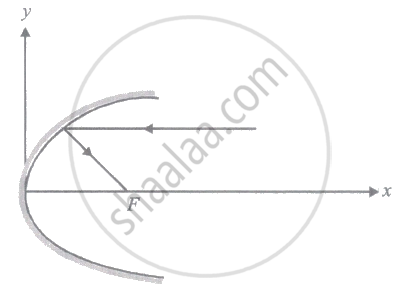
A parallel beam of light ray parallel to the x-axis is incident on a parabolic reflecting surface x = 2by2 as shown in the figure. After reflecting it passes through focal point F. What is the focal length of the reflecting surface?
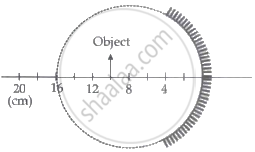
A spherical mirror is obtained as shown in the figure from a hollow glass sphere. if an object is positioned in front of the mirror, what will be the nature and magnification of the image of the object? (Figure drawn as schematic and not to scale)
If an object is placed at a distance of 10 cm in front of a concave mirror of a focal length of 20 cm, the image formed will be ______.
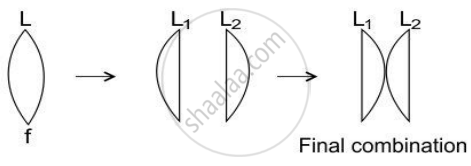
A lens of focal length f is divided into two equal parts and then these parts are put in a combination as shown in the figure below.
- What is the focal length of L1?
- What is the focal length of the final combination?