Advertisements
Advertisements
A 60 Ω resistor, a 1.0 H inductor and a 4 μF capacitor are connected in series to an ac supply generating an emf e = 300 sin (500t) V. Calculate:
- impedance of the circuit.
- peak value of the current flowing through the circuit.
- phase difference between the current and the supply voltage.
Concept: Combination of Cells in Series and in Parallel
An ac generator generates an emf which is given by e = 311 sin (240 πt) V. Calculate:
- frequency of the emf.
- r.m.s. value of the emf.
Concept: Cells, Emf, Internal Resistance
A meter bridge is balanced with a known resistance (R) in the left hand gap and an unknown resistance (S) in the right hand gap. Balance point is found to be at a distance of 1 cm from the left hand side. When the battery and the galvanometer are interchanged, balance point will ______.
Concept: Metre Bridge
Three identical cells each of emf 'e' are connected in parallel to form a battery. What is the emf of the battery?
Concept: Potentiometer
Three bulbs B1 (230V, 40W), B2 (230V, 60W) and B3 (230V, 100W) are connected in series to a 230V supply. Which bulb glows the brightest?
Concept: Combination of Resistors - Series and Parallel
The figure below shows two batteries, E1 and E2, having emfs of 18V and 10V and internal resistances of 1 Ω and 2 Ω, respectively. W1, W2 and W3 are uniform metallic wires AC, FD and BE having resistances of 8 Ω, 6 Ω and 10 Ω respectively. B and E are midpoints of the wires W1 and W2. Using Kirchhoff's laws of electrical circuits, calculate the current flowing in the wire W3:

Concept: Kirchhoff’s Rules
The Figure below shows a potentiometer circuit in which the driver cell D has an emf of 6 V and internal resistance of 2 Ω. The potentiometer wire AB is 10 m long and has a resistance of 28 Ω. The series resistance RS is of 2 Ω.
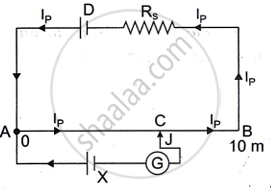
- The current Ip flowing in the potentiometer wire AB when the jockey (J) does not touch the wire AB.
- emf of the cell X if the balancing length AC is 4.5 m.
Concept: Potentiometer
Current I flowing through a metallic wire is gradually increased. Show graphically how heating power (P) developed in it varies with the current (I).
Concept: Flow of Electric Charges in a Metallic Conductor
In a potentiometer, a cell is balanced against 110 cm when the circuit is open. A cell is balanced at 100 cm when short-circuited through a resistance of 10 Ω. Find the internal resistance of the cell.
Concept: Potentiometer
Study the two circuits shown in the figure below. The cells in the two circuits are identical to each other. The resistance of the load resistor R is the same in both circuits.
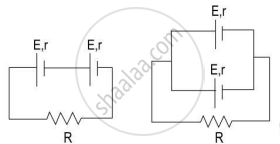
If the same current flows through the resistor R in both circuits, calculate the internal resistance of each cell in terms of the resistance of resistor R. Show your calculations.
Concept: Cells, Emf, Internal Resistance
The drift velocity of electrons in a conductor connected to a battery is given by vd = `(−"eE" τ)/"m"`. Here, e is the charge of the electron, E is the electric field, τ is the average time between collisions and m is the mass of the electron.
Based on this, answer the following:
- How does the drift velocity change with a change in the potential difference across the conductor?
- A copper wire of length 'l' is connected to a source. If the copper wire is replaced by another copper wire of the same area of cross-section but of length '4l', how will the drift velocity change? Explain your answer.
Concept: Drift of Electrons and the Origin of Resistivity
A circular coil carrying a current I has radius R and number of turns N. If all the three, i.e. the current
I, radius R and number of turns N are doubled, then, the magnetic field at its centre becomes:
(a) Double
(b) Half
(c) Four times
(d) One fourth
Concept: Magnetic Force
How will you convert a moving coil galvanometer into a voltmeter?
Concept: Moving Coil Galvanometer
A moving charged particle q travelling along the positive x-axis enters a uniform magnetic field B.
When will the force acting on q be maximum?
Concept: Force on a Moving Charge in Uniform Magnetic and Electric Fields
A long horizontal wire P carries a current of 50A. It is rigidly fixed. Another wire Q is placed directly above and parallel to P, as shown in Figure 1 below. The weight per unit length of the wire Q is 0.025 Nm-1 and it carries a current of 25A. Find the distance 'r' of the wire Q from the wire P so that the wire Q remains at rest
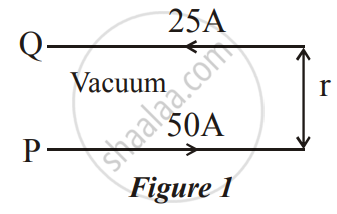
Concept: Force on a Moving Charge in Uniform Magnetic and Electric Fields
Explain the term hysteresis
Concept: Magnetic Force
Obtain an expression for magnetic flux density B at the centre of a circular coil of radius R, having N turns and carrying a current I
Concept: Magnetic Force
Why are the pole pieces of a horseshoe magnet in a moving coil galvanometer made cylinder in shape?
Concept: Moving Coil Galvanometer
An electric current I flows through an infinitely long conductor as shown in Figure 2 (a) below. Write an expression and direction for the magnetic field at point P.
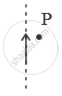
Concept: Magnetic Field Due to a Current Element, Biot-Savart Law
An electric current I flows through a circular loop as shown in Figure 2(b) below. Write an expression and direction for the magnetic field at the centre of the loop at point P.
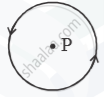
Concept: Magnetic Field Due to a Current Element, Biot-Savart Law
