Advertisements
Advertisements
A glass ball is dropped on a smooth horizontal floor from which it bounces to a height of 9m.On the second bounce it rises to a height of 6 m.From what height was the ball dropped and find the coefficient of restitution between the glass and the floor.
Given : First bounce height = 9 m
Second bounce height = 6 m
To find : Co-efficient of restitution
Concept: Velocity and Acceleration in Terms of Rectangular Co-ordinate System
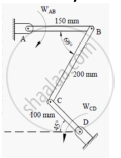
Angular velocity of connector BC is 4 r/s in clockwise direction.What is the angular velocities of cranks AB and CD?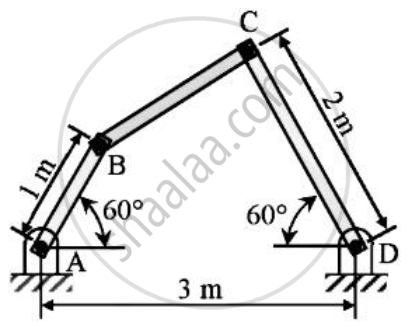
Concept: Velocity and Acceleration in Terms of Rectangular Co-ordinate System
The acceleration time diagram for a linear motion is shown. Construct velocity time diagram and displacement time diagram for the motion assuming that the motion starts with a initial velocity of 5 m/s from the starting point.

Given : Acceleration time graph
To draw : Velocity time graph
Displacement time graph
Concept: Velocity and Acceleration in Terms of Rectangular Co-ordinate System
Determine the speed at which the basket ball at A must be thrown at an angle 30o so that if makes it to the basket at B.
Also find at what speed it passes through the hoop.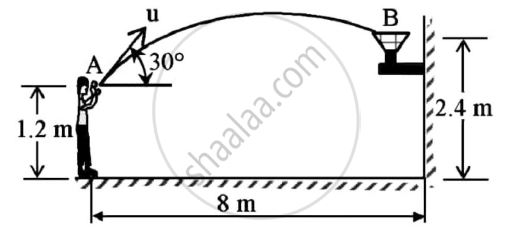
Concept: Motion Curves (a-t, v-t, s-t curves)
Figure shows a collar B which moves upwards with constant velocity of 1.5 m/s.At the instant when θ=50o.Determine :
(i)The angular velocity of rod pinned at B and freely resting at A against 25o sloping ground.
(ii)The velocity of end A of the rod.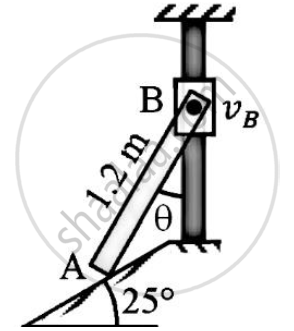
Concept: Motion Curves (a-t, v-t, s-t curves)
A circle of diameter 1.5 m is cut from a composite plate.Determine the centroid of the remaining area of plate.

Concept: Velocity and Acceleration in Terms of Rectangular Co-ordinate System
A rod AB has an angular velocity of 2 rad/sec,counter clock wise as shown.End C of rod BC is free to move on a horizontal surface.Determine:
(1)Angular velocity of rod BC
(2)Velocity of C
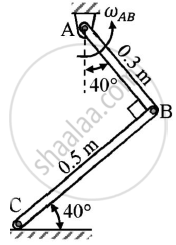
Given : ωAB=2 rad/sec (anti clockwise)
To find : ωBC
VC
Concept: Velocity and Acceleration in Terms of Rectangular Co-ordinate System
A shot is fired with a bullet with an initial velocity of 20 m/s from a point 10 m infront of a vertical wall 5 m high.
Find the angle of projection with the horizontal to enable the shot to just clear the wall. Also find the range of the shot where the bullet falls on the ground.
Given : u=20 m/s
Distance from wall=10m
Height of wall=5m
To find :Angle of projection
Range of shot
Concept: Projectile Motion
A particle falling under gravity travels 25 m in a particular second. Find the distance travelled by it in the next 3 seconds.
Given : Particle falls 25 m in a particular second
Sn=-25 m
u=0 m/s
To find : Distance travelled by it in next 3 seconds
Concept: Tangentialand Normal Component of Acceleration
Velocity-time diagram for a particle travelling along a straight line is shown in Figure 10. Draw acceleration-time and displacement-time diagram for the particle. Also find important values of acceleration and displacement.

Concept: Velocity and Acceleration in Terms of Rectangular Co-ordinate System
A 75kg person stands on a weighing scale in an elevator. 3 seconds after the motion starts from rest, the tension in the hoisting cable was found to be 8300N. Find the reading of the scale, in kg during this interval. Also find the velocity of the elevator at the end of this interval. The total mass of the elevator, including mass of the person and the weighing scale, is 750kg. If the elevator is now moving in the opposite direction, with same magnitude of acceleration, what will be the new reading of the scale?
Concept: Velocity and Acceleration in Terms of Rectangular Co-ordinate System
Two springs, each having stiffness of 0.6N/cm and length 20 cm are connected to a ball B of weight 50N. The initial tension developed in each spring is 1.6N. The arrangement is initially horizontal, as shown in Figure 14. If the ball is allowed to fall from rest, what will be its velocity at D, after it has fallen through a height of 15 cm?
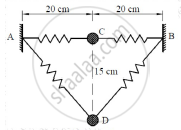
Concept: Velocity and Acceleration in Terms of Rectangular Co-ordinate System
Two balls, A (mass 3kg) and B (mass 4kg), are moving with velocities 25 m/s and 40 m/s respectively (Refer Figure 15). Before impact, the direction of velocity of two balls are 300 and 500 with the line joining their centers as shown in Figure 15. If coefficient of restitution for the impact is 0.78, find the magnitude and the direction of velocities of the balls after the impact.
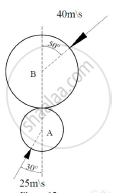
Concept: Velocity and Acceleration in Terms of Rectangular Co-ordinate System
A particle moves in x-y plane with acceleration components ax = -3m/s2 and ay = -16t m/s2. If its initial velocity is V0 = 50m/s directed at 350 to the x–axis, compute the radius of curvature of the path at t = 2 sec.
Concept: Tangentialand Normal Component of Acceleration
Find an expression for maximum range of a particle which is projected with an initial velocity of ‘u’ inclined at an angle of ‘β’ with the horizontal.
Concept: Motion Curves (a-t, v-t, s-t curves)
Compute the resultant of three forces acting on the plate shown in the figure. Locate it’s intersection with AB and BC.
Concept: Velocity Diagrams for Bodies in Plane Motion.
Rod AB of length 3 m is kept on a smooth plane as shown in the given figure.The velocity of end A is 5 m/s along the inclined plane.Locate the ICR and find velocity of end B.
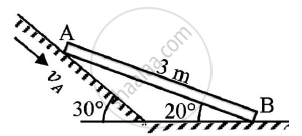
Given : Length of rod AB = 3m
va = 5 m/s
To find: ICR
Velocity of end B
Concept: Instantaneous Center of Rotation for the Velocity
Using Instantaneous Centre of Rotation (ICR) method, find the velocity of point A for the instant shown in Figure 2. Collar B moves along the vertical rod, whereas link AB moves along the plane which is inclined at 250. Ɵ = 450
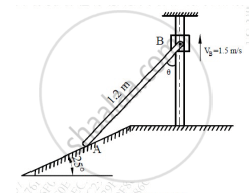
Concept: Instantaneous Center of Rotation for the Velocity
From the top of a tower, 28 m high, a stone is thrown vertically up with a velocity of 9m/s. After how much time will the stone reach the ground? With what velocity does it strike the ground?
Concept: Velocity Diagrams for Bodies in Plane Motion.
The link CD of the mechanism shown in Figure 7 is rotating in counterclockwise direction at an angular velocity of 5 rad/s. For the given instance, determine the angular velocity of link AB.
Concept: Instantaneous Center of Rotation for the Velocity
