Topics
Angle and Its Measurement
- Directed Angle
- Angles of Different Measurements
- Angles in Standard Position
- Measures of Angles
- Area of a Sector of a Circle
- Length of an Arc of a Circle
Trigonometry - 1
- Introduction of Trigonometry
- Trigonometric Functions with the Help of a Circle
- Signs of Trigonometric Functions in Different Quadrants
- Range of Cosθ and Sinθ
- Trigonometric Functions of Specific Angles
- Trigonometric Functions of Negative Angles
- Fundamental Identities
- Periodicity of Trigonometric Functions
- Domain and Range of Trigonometric Functions
- Graphs of Trigonometric Functions
- Polar Co-ordinate System
Trigonometry - 2
- Trigonometric Functions of Sum and Difference of Angles
- Trigonometric Functions of Allied Angels
- Trigonometric Functions of Multiple Angles
- Trigonometric Functions of Double Angles
- Trigonometric Functions of Triple Angle
- Factorization Formulae
- Formulae for Conversion of Sum Or Difference into Product
- Formulae for Conversion of Product in to Sum Or Difference
- Trigonometric Functions of Angles of a Triangle
Determinants and Matrices
- Definition and Expansion of Determinants
- Minors and Cofactors of Elements of Determinants
- Properties of Determinants
- Application of Determinants
- Determinant method
- Consistency of Three Equations in Two Variables
- Area of Triangle and Collinearity of Three Points
- Introduction of Matrices
- Types of Matrices
- Algebra of Matrices
- Properties of Matrix Multiplication
- Properties of Transpose of a Matrix
Straight Line
- Locus of a Points in a Co-ordinate Plane
- Straight Lines
- Equations of Line in Different Forms
- General Form of Equation of a Line
- Family of Lines
Circle
- Different Forms of Equation of a Circle
- General Equation of a Circle
- Parametric Form of a Circle
- Tangent
- Condition of tangency
- Tangents from a Point to the Circle
- Director circle
Conic Sections
- Double Cone
- Conic Sections
- Parabola
- Ellipse
- Hyperbola
Measures of Dispersion
- Meaning and Definition of Dispersion
- Measures of Dispersion
- Range of Data
- Variance
- Standard Deviation
- Change of Origin and Scale of Variance and Standard Deviation
- Standard Deviation for Combined Data
- Coefficient of Variation
Probability
- Basic Terminologies
- Event and Its Types
- Concept of Probability
- Addition Theorem for Two Events
- Conditional Probability
- Multiplication Theorem on Probability
- Independent Events
- Bayes’ Theorem
- Odds (Ratio of Two Complementary Probabilities)
Complex Numbers
- Introduction of Complex Number
- Concept of Complex Numbers
- Algebraic Operations of Complex Numbers
- Square Root of a Complex Number
- Fundamental Theorem of Algebra
- Argand Diagram Or Complex Plane
- De Moivres Theorem
- Cube Root of Unity
- Set of Points in Complex Plane
Sequences and Series
- Concept of Sequences
- Arithmetic Progression (A.P.)
- Geometric Progression (G. P.)
- Harmonic Progression (H. P.)
- Arithmetico Geometric Series
- Power Series
Permutations and Combination
- Fundamental Principles of Counting
- Invariance Principle
- Factorial Notation
- Permutations
- Permutations When All Objects Are Distinct
- Permutations When Repetitions Are Allowed
- Permutations When Some Objects Are Identical
- Circular Permutations
- Properties of Permutations
- Combination
- Properties of Combinations
Methods of Induction and Binomial Theorem
- Principle of Mathematical Induction
- Binomial Theorem for Positive Integral Index
- General Term in Expansion of (a + b)n
- Middle term(s) in the expansion of (a + b)n
- Binomial Theorem for Negative Index Or Fraction
- Binomial Coefficients
Sets and Relations
- Sets and Their Representations
- Types of Sets
- Operations on Sets
- Intervals
- Concept of Relation
Functions
- Concept of Functions
- Algebra of Functions
Limits
- Concept of Limits
- Factorization Method
- Rationalization Method
- Limits of Trigonometric Functions
- Substitution Method
- Limits of Exponential and Logarithmic Functions
- Limit at Infinity
Continuity
- Continuous and Discontinuous Functions
Differentiation
- Definition of Derivative and Differentiability
- Rules of Differentiation (Without Proof)
- Derivative of Algebraic Functions
- Derivatives of Trigonometric Functions
- Derivative of Logarithmic Functions
- Derivatives of Exponential Functions
- L' Hospital'S Theorem
Theorem
Theorem :
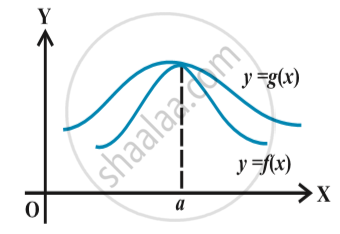
Let f and g be two real valued functions with the same domain such that f(x) ≤ g(x) for all x in the domain of definition, For some a, if both
`lim_( x -> a)` f(x) and `lim _(x - >a)` g(x) exist ,
then
`lim_(x ->a)` f(x) ≤ `lim_(x -> a)` g(x).
The explain in following fig.
Theorem
Theorem : (Sandwich Theorem)
Let f, g and h be real functions such that f (x) ≤ g( x) ≤ h(x) for all x in the common domain of definition. For some real number a , if
`lim_(x - > a)`f(x) = l = `lim_(x ->a)` h(x) , then `lim_(x ->a)` g(x) = l .fig.
Given below is a beautiful geometric proof of the following important inequality relating trigonometric functions.
`cos x < sin x/x < 1 for 0 <|x| < pi / 2`
Proof : We know that sin (– x) = – sin x and cos( – x) = cos x. Hence, it is sufficient to prove the inequality for 0 < x < `pi /2`. In the following fig.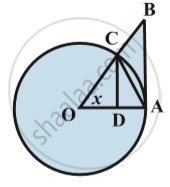
O is the centre of the unit circle such that the angle AOC is x radians and 0 < x <`pi /2` .Line segments B A and CD are perpendiculars to OA. Further, join AC. Then
Area of OAC ∆ < Area of sector OAC < Area of ∆ OAB .
i.e.,`1/2`OA.CD <`x / 2pi` .`( OA) ^2` < `1/2` OA .AB.
i.e., CD < x . OA < AB.
From ∆ OCD,
sin x = `(CD)/(OA)` (since OC = OA) and hence CD = OA sin x. Also tan x = `(AB)/(OA)` and hence AB = OA. tan x.
Thus OA sin x < OA. x < OA. tan x.
Since length OA is positive,
we have sin x < x < tan x.
Since 0 < x < `pi/2` , sinx is positive and thus by dividing throughout by sin x, we have `1 < x/(sin x) < 1/(cos x)` . Taking reciprocals throughout , we have
`cos x < (sin x)/x < 1`
which complete the proof.
Theorem
Theorem - The following are two important limits.
i) `lim_(x -> 0) sin x / x = 1`
ii) `lim_(x->0) (1 - cos x ) / x = 0`
Proof :
i) The inequality in (*) says that the function `sin x / x ` is sandwiched between the functions cos x and the constant function which takes value 1 .
Further, since `lim _(x→0)` cos x = 1, we see that the proof of (i) of the theorem is complete by sandwich theorem.
ii) we recall the trigonometric identity
1 – cos x = 2 `sin^2 (x / 2)`
Then
`lim_(x -> 0) (1 - cos x)/x = lim_(x -> 0) 2 sin^2 (x/2) / x = lim_(x-> 0) sin (x / 2) / (x / 2) . sin (x / 2)`
`lim_(x -> 0) sin(x / 2) / (x / 2) . lim_(x->0) sin (x/2) = 1.0 = 0`
Observe that we have implicitly used the fact that 0 x → is equivalent to `x/2 -> 0` . This may be justified by putting ` y = x / 2`
