Advertisements
Advertisements
प्रश्न
A = {1, 2, 3, 5} और B = {4, 6, 9}, A से B में एक सम्बन्ध R = {x, y} : x और y का
अंतर विषम है, x ∈ A, y ∈ B} द्वारा परिभाषित कीजिए। R को रोस्टर रूप में लिखिए।
उत्तर
दिया है: A = {1, 2, 3, 5} और B = {4, 6, 9}
R = {(x, y): x और y के बीच का अंतर विषम है; x ∈ A, y ∈ B}
= {(x, y) : y - x = odd; x ∈ A, y ∈ B}
∴ R = {(1, 4), (1, 6), (2, 9), (3, 4), (3, 6), (5, 4), (5, 6)}
APPEARS IN
संबंधित प्रश्न
मान लीजिए A= {1, 2, 3, ……. 14}, R = {(x, y): 3x – y = 0, जहाँ x, Y ∈ A) द्वारा A से A का एक संबंध R लिखिए। इसके प्रांत, सहप्रांत और परिसर लिखिए।
प्राकृत संख्याओं के समुच्चय पर R = {x, y) : y = x + 5, x संख्या 4 से कम, एक प्राकृत संख्या है, x,y ∈ N} द्वारा एक संबंध R परिभाषित कीजिए। इस संबंध को रोस्टर रूप में इसके प्रांत और परिसर लिखिए।
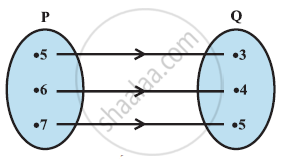
दी हुई आकृति समुच्चय P से Q का एक संबंध दर्शाती है।
इस संबंध को
- समुच्चय निर्माण रूप में
- रोस्टर रूप में लिखिए।
इसके प्रांत व परिसर क्या हैं?
मान लीजिए कि A= {1, 2, 3, 4, 6) मान लीजिए कि R, A पर {(a, b) : a, b ϵ A, संख्या a संख्या b को यथावथ विभाजित करती है} द्वारा परिभाषित एक संबंध है।
- R को रोस्टर रूप में लिखिए।
- R का प्रांत ज्ञात कीजिए।
- R का परिसर ज्ञात कीजिए।
मान लीजिए कि A = {x, y, z} और B = {1, 2}, A से B के संबंधों की संख्या ज्ञात कीजिए।
संबंध f, \[f\left( x \right) = \begin{cases}x^2 , & 0 \leq x \leq 3 \\ 3x, & 3 \leq x \leq 10\end{cases}\] द्वारा परिभाषित है।
संबंध g, \[g\left( x \right) = \begin{cases}x^2 , & 0 \leq x \leq 2 \\ 3x, & 2 \leq x \leq 10\end{cases}\] द्वारा परिभाषित है।
दर्शाइए कि क्यों f एक फलन है और g फलन नहीं है।
मान लीजिए A = {1, 2, 3, 4}, B = {1, 5, 9, 11, 15, 16} और f= {(1, 5), (2, 9), (3, 1), (4, 5), (2, 11)}, क्या निम्नलिखित कथन सत्य है?
f, A से B में एक संबंध है।
दशा में अपने उत्तर का औचित्य बताइए।
मान लीजिए कि A तथा B कोई ऐसे दो समुच्चय हैं कि n(B) = p, n(A) = q, तो समुच्चयों f : A → B कुल संख्या ______ है।
दिया हुआ है, A = {1, 2, 3, 4, 5}, S = {(x, y) : x ∈ A, y ∈ A} तो उन क्रमित युग्मों को ज्ञात कीजिए, जो निम्नलिखित प्रतिबंध को संतुष्ट करता हैं: x + y = 5
दिया हुआ है, A = {1, 2, 3, 4, 5}, S = {(x, y) : x ∈ A, y ∈ A} तो उन क्रमित युग्मों को ज्ञात कीजिए, जो निम्नलिखित प्रतिबंध को संतुष्ट करता हैं: x + y > 8
यदि R2 = {(x, y) ∣ x और y पूर्णांक हैं और x2 + y2 = 64} एक संबंध है, तो R2 ज्ञात कीजिए (रोस्टर रूप में लिखिए)।
यदि R3 = {(x, ∣x∣) ∣ x एक वास्तविक संख्या है} एक संबंध है, तो R3 का प्रांत तथा परिसर ज्ञात कीजिए।
क्या नीचे दिये गये संबंध फलन हैं? अपने उत्तर का औचित्य भी बताइए:
h = {(4, 6), (3, 9), (−11, 6), (3, 11)}
क्या नीचे दिये गये संबंध फलन हैं? अपने उत्तर का औचित्य भी बताइए:
t = {(x, 3) ∣ x एक वास्तविक संख्या है}
नीचे दिये फलन का प्रांत ज्ञात कीजिए:
f(x) = `1/sqrt(1 - cosx)`
नीचे दिये फलन का प्रांत ज्ञात कीजिए:
f(x) = x|x|
नीचे दिये फलन का प्रांत ज्ञात कीजिए:
f(x) = `(x^3 - x + 3)/(x^2 - 1)`
नीचे दिये फलन का प्रांत ज्ञात कीजिए:
f(x) = `(3x)/(2x - 8)`
नीचे दिये फलन का परिसर ज्ञात कीजिए:
f(x) = `3/(2 - x^2)`
फलन f(x) = `1/sqrt(x−5)` का प्रांत तथा परिसर ज्ञात कीजिए।
f(x) = `1/(1 - 2cosx)` का परिसर ______ है।
यदि f(x) = ax + b, जहाँ a और b पूर्णांक हैं। यदि f(-1) = -5 और f(3) = 3, तो ______
बताइए कि प्रश्न संख्या में दिये कथन सत्य हैं या असत्य है:
यदि (x − 2, y + 5) = `(−2, 1/3)`, तो x = 4, y = `(−14)/3`
R = {(a, b) : a, b ∈ N तथा a = b2} द्वारा परिभाषित N से N में, एक संबंध R है। क्या निम्नलिखित कथन सत्य है।
(a,b) ∈ R, (b, c) ∈ R का तात्पर्य है कि (a, c) ∈ R?
दशा में अपने उत्तर का औचित्य भी बताइए।
