Advertisements
Advertisements
प्रश्न
A person buys a lottery ticket in 50 lotteries, in each of which his chance of winning a prize is 1/100. What is the probability that he will in a prize (a) at least once (b) exactly once (c) at least twice?
उत्तर
Let X represent the number of winning prizes in 50 lotteries. The trials are Bernoulli trials.
Clearly, X has a binomial distribution with n = 50 and p = 1/100
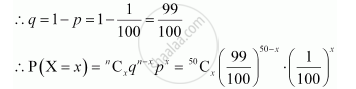
(a) P (winning at least once) = P (X ≥ 1)

(b) P (winning exactly once) = P(X = 1)
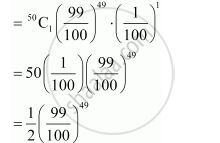
(c) P (at least twice) = P(X ≥ 2)
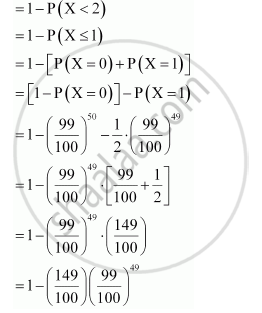
APPEARS IN
संबंधित प्रश्न
Given X ~ B (n, p)
If n = 10 and p = 0.4, find E(X) and var (X).
A pair of dice is thrown 4 times. If getting a doublet is considered a success, find the probability of two successes.
There are 5% defective items in a large bulk of items. What is the probability that a sample of 10 items will include not more than one defective item?
Five cards are drawn successively with replacement from a well-shuffled deck of 52 cards. What is the probability that
- all the five cards are spades?
- only 3 cards are spades?
- none is a spade?
On a multiple choice examination with three possible answers for each of the five questions, what is the probability that a candidate would get four or more correct answers just by guessing?
Find the probability of throwing at most 2 sixes in 6 throws of a single die.
In a box containing 100 bulbs, 10 are defective. The probability that out of a sample of 5 bulbs, none is defective is
(A) 10−1
(B) `(1/2)^5`
(C) `(9/10)^5`
(D) 9/10
A couple has two children, Find the probability that both children are females, if it is known that the elder child is a female.
In a hurdle race, a player has to cross 10 hurdles. The probability that he will clear each hurdle is 5/6 . What is the probability that he will knock down fewer than 2 hurdles?
Five cards are drawn one by one, with replacement, from a well-shuffled deck of 52 cards. Find the probability that
(i) all the five cards diamonds
(ii) only 3 cards are diamonds
(iii) none is a diamond
A bag contains 10 balls, each marked with one of the digits from 0 to 9. If four balls are drawn successively with replacement from the bag, what is the probability that none is marked with the digit 0?
An unbiased die is thrown twice. A success is getting a number greater than 4. Find the probability distribution of the number of successes.
The probability that a student entering a university will graduate is 0.4. Find the probability that out of 3 students of the university only one will graduate .
The probability that a student entering a university will graduate is 0.4. Find the probability that out of 3 students of the university all will graduate .
From a lot of 30 bulbs that includes 6 defective bulbs, a sample of 4 bulbs is drawn at random with replacement. Find the probability distribution of the number of defective bulbs.
Find the probability that in 10 throws of a fair die, a score which is a multiple of 3 will be obtained in at least 8 of the throws.
A die is thrown 5 times. Find the probability that an odd number will come up exactly three times.
The probability of a man hitting a target is 0.25. He shoots 7 times. What is the probability of his hitting at least twice?
Can the mean of a binomial distribution be less than its variance?
A dice is thrown thrice. A success is 1 or 6 in a throw. Find the mean and variance of the number of successes.
If X follows a binomial distribution with mean 4 and variance 2, find P (X ≥ 5).
A die is thrown three times. Let X be 'the number of twos seen'. Find the expectation of X.
If the mean and variance of a random variable X with a binomial distribution are 4 and 2 respectively, find P (X = 1).
A rifleman is firing at a distant target and has only 10% chance of hitting it. The least number of rounds he must fire in order to have more than 50% chance of hitting it at least once is
One hundred identical coins, each with probability p of showing heads are tossed once. If 0 < p < 1 and the probability of heads showing on 50 coins is equal to that of heads showing on 51 coins, the value of p is
The least number of times a fair coin must be tossed so that the probability of getting at least one head is at least 0.8, is
A biased coin with probability p, 0 < p < 1, of heads is tossed until a head appears for the first time. If the probability that the number of tosses required is even is 2/5, then p equals
In a binomial distribution, the probability of getting success is 1/4 and standard deviation is 3. Then, its mean is
Mark the correct alternative in the following question:
The probability of guessing correctly at least 8 out of 10 answers of a true false type examination is
A bag contains 7 red, 5 white and 8 black balls. If four balls are drawn one by one with replacement, what is the probability that any two are white ?
The probability that a bulb produced by a factory will fuse after 150 days of use is 0.05. Find the probability that out of 5 such bulbs at least one will fuse after 150 days of use
For Bernoulli Distribution, state formula for E(X) and V(X).
Which one is not a requirement of a binomial distribution?
A pair of dice is thrown four times. If getting a doublet is considered a success then find the probability of two success.
An ordinary dice is rolled for a certain number of times. If the probability of getting an odd number 2 times is equal to the probability of getting an even number 3 times, then the probability of getting an odd number for odd number of times is ______.
If X ∼ B(n, p), n = 6 and 9 P(X = 4) = P(X = 2), then find the value of p.
