Advertisements
Advertisements
प्रश्न
A person buys a lottery ticket in 50 lotteries, in each of which his chance of winning a prize is 1/100. What is the probability that he will in a prize (a) at least once (b) exactly once (c) at least twice?
उत्तर
Let X represent the number of winning prizes in 50 lotteries. The trials are Bernoulli trials.
Clearly, X has a binomial distribution with n = 50 and p = 1/100
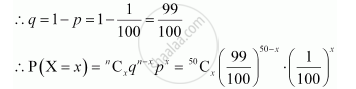
(a) P (winning at least once) = P (X ≥ 1)

(b) P (winning exactly once) = P(X = 1)
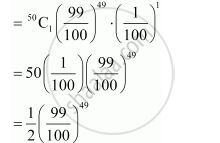
(c) P (at least twice) = P(X ≥ 2)
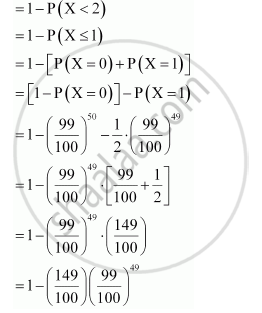
APPEARS IN
संबंधित प्रश्न
A fair coin is tossed 8 times. Find the probability that it shows heads at least once
A pair of dice is thrown 4 times. If getting a doublet is considered a success, find the probability of two successes.
Find the probability of getting 5 exactly twice in 7 throws of a die.
It is known that 10% of certain articles manufactured are defective. What is the probability that in a random sample of 12 such articles, 9 are defective?
In a box containing 100 bulbs, 10 are defective. The probability that out of a sample of 5 bulbs, none is defective is
(A) 10−1
(B) `(1/2)^5`
(C) `(9/10)^5`
(D) 9/10
A couple has two children, Find the probability that both children are males, if it is known that at least one of the children is male.
The probability that a student is not a swimmer is 1/5 . Then the probability that out of five students, four are swimmers is
(A) `""^5C_4 (4/5)^4 1/5`
(B) `(4/5)^4 1/5
(C) `""^5C_1 1/5 (4/5)^4 `
(D) None of these
A box contains 100 tickets, each bearing one of the numbers from 1 to 100. If 5 tickets are drawn successively with replacement from the box, find the probability that all the tickets bear numbers divisible by 10.
A bag contains 10 balls, each marked with one of the digits from 0 to 9. If four balls are drawn successively with replacement from the bag, what is the probability that none is marked with the digit 0?
A coin is tossed 5 times. If X is the number of heads observed, find the probability distribution of X.
The probability that a certain kind of component will survive a given shock test is \[\frac{3}{4} .\] Find the probability that among 5 components tested at most 3 will survive .
Assume that the probability that a bomb dropped from an aeroplane will strike a certain target is 0.2. If 6 bombs are dropped, find the probability that at least 2 will strike the target
In a hospital, there are 20 kidney dialysis machines and the chance of any one of them to be out of service during a day is 0.02. Determine the probability that exactly 3 machines will be out of service on the same day.
The probability of a shooter hitting a target is \[\frac{3}{4} .\] How many minimum number of times must he/she fire so that the probability of hitting the target at least once is more than 0.99?
A pair of dice is thrown 4 times. If getting a doublet is considered a success, find the probability distribution of the number of successes.
Find the probability that in 10 throws of a fair die, a score which is a multiple of 3 will be obtained in at least 8 of the throws.
A box has 20 pens of which 2 are defective. Calculate the probability that out of 5 pens drawn one by one with replacement, at most 2 are defective.
The mean and variance of a binomial variate with parameters n and p are 16 and 8, respectively. Find P (X = 0), P (X = 1) and P (X ≥ 2).
Find the expected number of boys in a family with 8 children, assuming the sex distribution to be equally probable.
In a binomial distribution, if n = 20 and q = 0.75, then write its mean.
If the mean of a binomial distribution is 20 and its standard deviation is 4, find p.
An unbiased coin is tossed 4 times. Find the mean and variance of the number of heads obtained.
If in a binomial distribution n = 4, P (X = 0) = \[\frac{16}{81}\], then P (X = 4) equals
A fair coin is tossed a fixed number of times. If the probability of getting seven heads is equal to that of getting nine heads, the probability of getting two heads is
A five-digit number is written down at random. The probability that the number is divisible by 5, and no two consecutive digits are identical, is
If the mean and variance of a binomial distribution are 4 and 3, respectively, the probability of getting exactly six successes in this distribution is
A coin is tossed 4 times. The probability that at least one head turns up is
A coin is tossed n times. The probability of getting at least once is greater than 0.8. Then, the least value of n, is
The probability of selecting a male or a female is same. If the probability that in an office of n persons (n − 1) males being selected is \[\frac{3}{2^{10}}\] , the value of n is
Mark the correct alternative in the following question:
Suppose a random variable X follows the binomial distribution with parameters n and p, where 0 < p < 1. If \[\frac{P\left( X = r \right)}{P\left( X = n - r \right)}\] is independent of n and r, then p equals
Mark the correct alternative in the following question:
Which one is not a requirement of a binomial dstribution?
A bag contains 7 red, 5 white and 8 black balls. If four balls are drawn one by one with replacement, what is the probability that all are white ?
A bag contains 7 red, 5 white and 8 black balls. If four balls are drawn one by one with replacement, what is the probability that any two are white ?
The probability that a bulb produced by a factory will fuse after 150 days of use is 0.05. Find the probability that out of 5 such bulbs not more than one will fuse after 150 days of use
Bernoulli distribution is a particular case of binomial distribution if n = ______
An ordinary dice is rolled for a certain number of times. If the probability of getting an odd number 2 times is equal to the probability of getting an even number 3 times, then the probability of getting an odd number for odd number of times is ______.
The mean and variance of a binomial distribution are α and `α/3` respectively. If P(X = 1) = `4/243`, then P(X = 4 or 5) is equal to ______.
A fair coin is tossed 8 times. Find the probability that it shows heads at most once.
A fair coin is tossed 6 times. Find the probability of getting heads 4 times.
