Advertisements
Advertisements
प्रश्न
A rhombus shaped field has green grass for 18 cows to graze. If each side of the rhombus is 30 m and its longer diagonal is 48 m, how much area of grass field will each cow be getting?
Advertisements
उत्तर
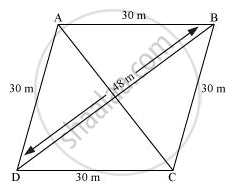
Let ABCD be a rhombus-shaped field.
For ΔBCD,
Semi-perimeter,
`s=(48+30+30)/2 = 54 m`
By Heron's Formula,
`"Area of triangle "=sqrt(s(s-a)(s-b)(s-c))`
`therefore" Area of ΔBCD "=[sqrt(54(54-48)(54-30)(54-30))]m^2`
`=sqrt(54(6)(24)(24))`
= 3 x 6 x 24
= 432 m2
Area of field = 2 × Area of ΔBCD
= (2 × 432) m2 = 864 m2
Area for grazing for 1 cow = 864/18 = 48 m2
Each cow will get 48 m2 area of grass field.
संबंधित प्रश्न
A park, in the shape of a quadrilateral ABCD, has ∠C = 90°, AB = 9 m, BC = 12 m, CD = 5 m and AD = 8 m. How much area does it occupy?
A triangle and a parallelogram have the same base and the same area. If the sides of triangle are 26 cm, 28 cm and 30 cm, and the parallelogram stands on the base 28 cm, find the height of the parallelogram.
Two parallel side of a trapezium are 60 cm and 77 cm and other sides are 25 cm and 26 cm. Find the area of the trapezium.
Find the area of a quadrilateral ABCD in which AD = 24 cm, ∠BAD = 90° and BCD forms an equilateral triangle whose each side is equal to 26 cm. (Take √3 = 1.73)
Find the perimeter and area of the quadrilateral ABCD in which AB = 17 cm, AD =9 cm, CD = l2cm, ∠ACB = 90° and AC=l5cm.
Mark the correct alternative in each of the following:
The sides of a triangle are 16 cm, 30 cm, 34 cm. Its area is
The sides of a triangle are 7 cm, 9 cm and 14 cm. Its area is
In the given figure, the ratio AD to DC is 3 to 2. If the area of Δ ABC is 40 cm2, what is the area of Δ BDC?
Find the area of a quadrilateral ABCD whose sides are AB = 13 cm, BC = 12 cm, CD = 9 cm, AD = 14 cm and diagonal BD = 15 cm
A park is in the shape of a quadrilateral. The sides of the park are 15 m, 20 m, 26 m and 17 m and the angle between the first two sides is a right angle. Find the area of the park
