Advertisements
Advertisements
प्रश्न
ABCD एक समचतुर्भुज है और P, Q, R और S क्रमशः भुजाओं AB, BC, CD और DA के मध्य-बिंदु है। दर्शाइए कि चतुर्भुज PQRS एक आयत है।
उत्तर
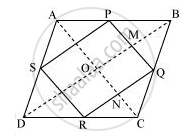
ΔABC में, P और Q क्रमशः भुजाओं AB और BC के मध्य-बिंदु हैं।
PQ || AC और PQ = `1/2AC` ...(मध्य-बिंदु प्रमेय का उपयोग करके) ...(1)
ΔADC में,
R और S क्रमशः CD और AD के मध्य-बिंदु हैं।
∴ RS || AC और RS = `1/2 AC` ...(मध्य-बिंदु प्रमेय का उपयोग करके) ...(2)
समीकरण (1) और (2) से, हम प्राप्त करते हैं
PQ || RS और PQ = RS
चूँकि चतुर्भुज PQRS में, सम्मुख भुजाओं का एक युग्म बराबर और समांतर होता है एक दूसरे को, यह एक समांतर चतुर्भुज है।
मान लीजिए समचतुर्भुज ABCD के विकर्ण एक दूसरे को बिंदु O पर प्रतिच्छेद करते हैं।
चतुर्भुज OMQN में,
MQ || ON ...(∵ PQ || AC)
QN || OM ...(∵ QR || BD)
अतः OMQN एक समांतर चतुर्भुज है।
⇒ ∠MQN = ∠NOM
⇒ ∠PQR = ∠NOM
हालाँकि, ∠NOM = 90° ...(एक समचर्तुभुज के विकर्ण परस्पर लंब हैं।)
∴ ∠PQR = 90°
स्पष्टत:, PQRS एक समांतर चतुर्भुज है जिसका एक अंत: कोण 90° है।
अत:, PQRS एक आयत है।
APPEARS IN
संबंधित प्रश्न
ABCD एक आयत है, जिसमें P, Q, R और S क्रमश: भुजाओं AB, BC, CD और DA के मध्य-बिंदु हैं। दर्शाइए कि चतुर्भुज PQRS एक समचतुर्भुज है।
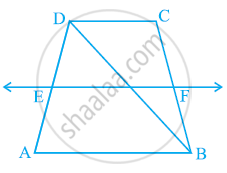
ABCD एक समलंब है, जिसमें AB || DC है। साथ ही, BD एक विकर्ण है और E भुजा AD का मध्य-बिंदु है। E से होकर एक रेखा AB के समांतर खींची गई है, जो BC को F पर प्रतिच्छेद करती है (देखिए आकृति में)। दर्शाइए कि F भुजा BC का मध्य-बिंदु है।
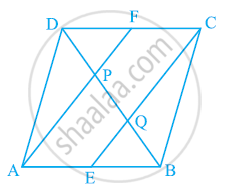
एक समांतर चतुर्भुज ABCD में E और F क्रमश: भुजाओं AB और CD के मध्य-बिंदु हैं (देखिए आकृति में)। दर्शाइए कि रेखाखंड AF और EC विकर्ण BD को समत्रिभाजित करते हैं।
दर्शाइए कि किसी चतुर्भुज की सम्मुख भुजाओं के मध्य-बिंदुओं को मिलाने वाले रेखाखंड परस्पर समद्विभाजित करते हैं।
D, E और F क्रमश: एक समबाहु त्रिभुज ABC की भुजाओं BC, CA और AB के मध्य-बिंदु हैं। दर्शाइए कि ∆DEF भी एक समबाहु त्रिभुज है।
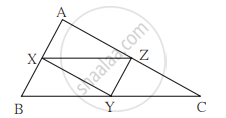
आकृति में ΔABC मे बिंदु X, Y, Z यह क्रमशः भुजाओं AB, BC तथा AC के मध्यबिंदु है। AB = 5 सेमी, AC = 9 सेमी तथा BC = 11 सेमी, तो XY, YZ, XZ की लंबाई ज्ञात कीजिए।
आकृति में `square` PQRS तथा `square` MNRL आयत है। बिंदु M यह PR का मध्यबिंदु है। तो सिद्ध कीजिए कि
(i) SL = LR, (ii) LN = `1/2` SQ

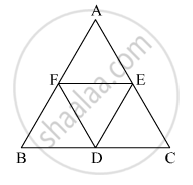
आकृति में ΔABC समबाहु त्रिभुज है जिसमें बिंदु F, D, E यह क्रमशः भुजा AB, भुजा BC, भुजा AC के मध्यबिंदु हैं तो सिद्ध कीजिए कि ΔFED यह समबाहु त्रिभुज है।
आकृति में रेख PD यह ΔPQR की माध्यिका है। बिंदु T यह PD का मध्यबिंदु है। QT को आगे बढ़ाने पर यह PR को बिंदु M पर प्रतिच्छेदित करता है। तो सिदघ कीजिए कि `"PR"/"PM" = 1/3`
[सूचना: DN || QM खींचें।]

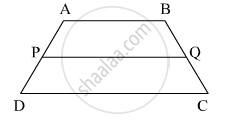
संलग्न आकृति में `square` ABCD समलंब चतुर्भुज है। AB || DC है। रेख AD तथा रेख BC के मध्यबिंदु क्रमशः P तथा Q हैं, तो सिद्ध कीजिए कि PQ || AB तथा PQ = `1/2` (AB + DC)