Advertisements
Advertisements
प्रश्न
An urn contains 5 red and 2 black balls. Two balls are randomly drawn. Let X represents the number of black balls. What are the possible values of X? Is X a random variable?
उत्तर
The two balls selected can be represented as BB, BR, RB, RR, where B represents a black ball and R represents a red ball.
X represents the number of black balls.
∴X (BB) = 2
X (BR) = 1
X (RB) = 1
X (RR) = 0
Therefore, the possible values of X are 0, 1, and 2.
Yes, X is a random variable.
APPEARS IN
संबंधित प्रश्न
A random variable X has the following probability distribution:
then E(X)=....................
Of the students in a college, it is known that 60% reside in hostel and 40% are day scholars (not residing in hostel). Previous year results report that 30% of all students who reside in hostel attain A grade and 20% of day scholars attain A grade in their annual examination. At the end of the year, one student is chosen at random from the college and he has an A grade, what is the probability that the student is hostler?
Two dice are thrown simultaneously. If X denotes the number of sixes, find the expectation of X.
Three persons A, B and C shoot to hit a target. If A hits the target four times in five trials, B hits it three times in four trials and C hits it two times in three trials, find the probability that:
1) Exactly two persons hit the target.
2) At least two persons hit the target.
3) None hit the target.
Find the probability distribution of the number of doublets in four throws of a pair of dice. Also find the mean and variance of this distribution.
A random variable X takes the values 0, 1, 2 and 3 such that:
P (X = 0) = P (X > 0) = P (X < 0); P (X = −3) = P (X = −2) = P (X = −1); P (X = 1) = P (X = 2) = P (X = 3) . Obtain the probability distribution of X.
Four cards are drawn simultaneously from a well shuffled pack of 52 playing cards. Find the probability distribution of the number of aces.
Five defective mangoes are accidently mixed with 15 good ones. Four mangoes are drawn at random from this lot. Find the probability distribution of the number of defective mangoes.
Two cards are drawn successively with replacement from a well shuffled pack of 52 cards. Find the probability distribution of the number of kings.
Find the probability distribution of the number of white balls drawn in a random draw of 3 balls without replacement, from a bag containing 4 white and 6 red balls
An urn contains 4 red and 3 blue balls. Find the probability distribution of the number of blue balls in a random draw of 3 balls with replacement.
Let X represent the difference between the number of heads and the number of tails when a coin is tossed 6 times. What are the possible values of X?
The probability distribution of a random variable X is given below:
| x | 0 | 1 | 2 | 3 |
| P(X) | k |
\[\frac{k}{2}\]
|
\[\frac{k}{4}\]
|
\[\frac{k}{8}\]
|
Find P(X ≤ 2) + P(X > 2) .
Two bad eggs are accidently mixed up with ten good ones. Three eggs are drawn at random with replacement from this lot. Compute the mean for the number of bad eggs drawn.
Three cards are drawn at random (without replacement) from a well shuffled pack of 52 cards. Find the probability distribution of number of red cards. Hence, find the mean of the distribution .
In a game, a man wins Rs 5 for getting a number greater than 4 and loses Rs 1 otherwise, when a fair die is thrown. The man decided to thrown a die thrice but to quit as and when he gets a number greater than 4. Find the expected value of the amount he wins/loses.
For what value of k the following distribution is a probability distribution?
| X = xi : | 0 | 1 | 2 | 3 |
| P (X = xi) : | 2k4 | 3k2 − 5k3 | 2k − 3k2 | 3k − 1 |
From a lot of 15 bulbs which include 5 defective, a sample of 4 bulbs is drawn one by one with replacement. Find the probability distribution of number of defective bulbs. Hence, find the mean of the distribution.
A die is tossed twice. A 'success' is getting an even number on a toss. Find the variance of number of successes.
An urn contains 3 white and 6 red balls. Four balls are drawn one by one with replacement from the urn. Find the probability distribution of the number of red balls drawn. Also find mean and variance of the distribution.
Verify the following function, which can be regarded as p.m.f. for the given values of X :
| X = x | -1 | 0 | 1 |
| P(x) | -0.2 | 1 | 0.2 |
Find mean and standard deviation of the continuous random variable X whose p.d.f. is given by f(x) = 6x(1 - x);= (0); 0 < x < 1(otherwise)
The expenditure Ec of a person with income I is given by Ec = (0.000035) I2 + (0. 045) I. Find marginal propensity to consume (MPC) and average propensity to consume (APC) when I = 5000.
Verify whether the following function can be regarded as probability mass function (p.m.f.) for the given values of X :
| X | -1 | 0 | 1 |
| P(X = x) | -0.2 | 1 | 0.2 |
The probability that a bomb dropped from an aeroplane will strike a target is `1/5`, If four bombs are dropped, find the probability that :
(a) exactly two will strike the target,
(b) at least one will strike the target.
An urn contains 5 red and 2 black balls. Two balls are drawn at random. X denotes number of black balls drawn. What are possible values of X?
Determine whether each of the following is a probability distribution. Give reasons for your answer.
| y | –1 | 0 | 1 |
| P(y) | 0.6 | 0.1 | 0.2 |
A sample of 4 bulbs is drawn at random with replacement from a lot of 30 bulbs which includes 6 defective bulbs. Find the probability distribution of the number of defective bulbs.
A die is thrown 4 times. If ‘getting an odd number’ is a success, find the probability of at least 3 successes
A pair of dice is thrown 3 times. If getting a doublet is considered a success, find the probability of two successes
Find the probability of throwing at most 2 sixes in 6 throws of a single die.
Solve the following problem :
Following is the probability distribution of a r.v.X.
| X | – 3 | – 2 | –1 | 0 | 1 | 2 | 3 |
| P(X = x) | 0.05 | 0.1 | 0.15 | 0.20 | 0.25 | 0.15 | 0.1 |
Find the probability that X is positive.
Solve the following problem :
Following is the probability distribution of a r.v.X.
| x | – 3 | – 2 | –1 | 0 | 1 | 2 | 3 |
| P(X = x) | 0.05 | 0.1 | 0.15 | 0.20 | 0.25 | 0.15 | 0.1 |
Find the probability that X is non-negative
Solve the following problem :
In a large school, 80% of the students like mathematics. A visitor asks each of 4 students, selected at random, whether they like mathematics.
Find the probability that the visitor obtains the answer yes from at least 3 students.
Find the probability distribution of the maximum of the two scores obtained when a die is thrown twice. Determine also the mean of the distribution.
The probability distribution of a random variable x is given as under:
P(X = x) = `{{:("k"x^2, "for" x = 1"," 2"," 3),(2"k"x, "for" x = 4"," 5"," 6),(0, "otherwise"):}`
where k is a constant. Calculate E(X)
For the following probability distribution:
| X | 1 | 2 | 3 | 4 |
| P(X) | `1/10` | `3/10` | `3/10` | `2/5` |
E(X2) is equal to ______.
A large chain retailer purchases an electric device from the manufacturer. The manufacturer indicates that the defective rate of the device is 10%. The inspector of the retailer randomly selects 4 items from a shipment. Complete the following activity to find the probability that the inspector finds at most one defective item in the 4 selected items.
Solution:
Here, n = 4
p = probability of defective device = 10% = `10/100 = square`
∴ q = 1 - p = 1 - 0.1 = `square`
X ∼ B(4, 0.1)
`P(X=x)=""^n"C"_x p^x q^(n-x)= ""^4"C"_x (0.1)^x (0.9)^(4 - x)`
P[At most one defective device] = P[X ≤ 1]
= P[X=0] + P[X=1]
= `square+square`
∴ P[X ≤ 1] = `square`
Kiran plays a game of throwing a fair die 3 times but to quit as and when she gets a six. Kiran gets +1 point for a six and –1 for any other number.
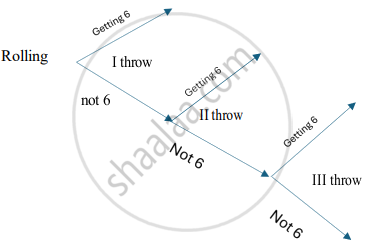
- If X denotes the random variable “points earned” then what are the possible values X can take?
- Find the probability distribution of this random variable X.
- Find the expected value of the points she gets.
