Advertisements
Advertisements
рдкреНрд░рд╢реНрди
Complete the activity to find the value of x.
3x + 2y = 11 …(i) and 2x + 3y = 4 …(ii)
Solution:
Multiply equation (i) by _______ and equation (ii) by _______.
`square` × (3x + 2y = 11) ∴ 9x + 6y = 33 …(iii)
`square` × (2x + 3y = 4) ∴ 4x + 6y = 8 …(iv)
Subtract (iv) from (iii),
`square` x = 25
∴ x = `square`
рдЙрддреНрддрд░
3x + 2y = 11 …(i) and 2x + 3y = 4 …(ii)
Multiply equation (i) by 3 and equation (ii) by 2.
3 × (3x + 2y = 11) ∴ 9x + 6y = 33 …(iii)
2 × (2x + 3y = 4) ∴ 4x + 6y = 8 …(iv)
Subtract (iv) from (iii),
5 x = 25
∴ x = `25/5`
∴ x = 5
APPEARS IN
рд╕рдВрдмрдВрдзрд┐рдд рдкреНрд░рд╢реНрди
A thief runs with a uniform speed of 100 m/minute. After one minute, a policeman runs after the thief to catch him. He goes with a speed of 100 m/minute in the first minute and increases his speed by 10 m/minute every succeeding minute. After how many minutes the policeman will catch the thief.
Solve the following system of equations by the method of cross-multiplication. `\frac{a}{x}-\frac{b}{y}=0;\text{}\frac{ab^{2}}{x}+\frac{a^{2}b}{y}=a^{2}+b^{2};` Where x ≠ 0, y ≠ 0
Which of the following pairs of linear equations has unique solution, no solution, or infinitely many solutions. In case there is a unique solution, find it by using cross multiplication method
x – 3y – 3 = 0
3x – 9y – 2 = 0
Which of the following pairs of linear equations has unique solution, no solution or infinitely many solutions? In case there is a unique solution, find it by using cross multiplication method
2x + y = 5
3x + 2y = 8
Solve the following systems of equations:
4u + 3y = 8
`6u - 4y = -5`
Solve the following systems of equations:
`3x - (y + 7)/11 + 2 = 10`
`2y + (x + 10)/7 = 10`
Solve the following systems of equations:
`10/(x + y) + 2/(x - y) = 4`
`15/(x + y) - 5/(x - y) = -2`
Solve each of the following systems of equations by the method of cross-multiplication :
2x + y = 35
3x + 4y = 65
Solve each of the following systems of equations by the method of cross-multiplication :
`57/(x + y) + 6/(x - y) = 5`
`38/(x + y) + 21/(x - y) = 9`
Solve each of the following systems of equations by the method of cross-multiplication :
`a^2/x - b^2/y = 0`
`(a^2b)/x + (b^2a)/y = a + b, x , y != 0`
Solve each of the following systems of equations by the method of cross-multiplication :
`(ax)/b - (by)/a = a + b`
ax - by = 2ab
Solve each of the following systems of equations by the method of cross-multiplication :
`b/a x + a/b y - (a^2 + b^2) = 0`
x + y - 2ab = 0
Solve the system of equations by using the method of cross multiplication:
6x - 5y - 16 = 0,
7x - 13y + 10 = 0
Solve the system of equations by using the method of cross multiplication:
2ax + 3by – (a + 2b) = 0,
3ax + 2by – (2a + b) = 0
Find the values of x and y in the following rectangle [see figure].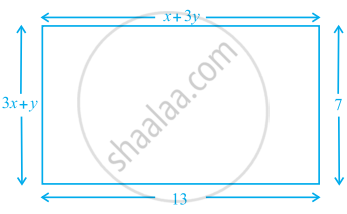
Solve the following pair of equations:
x + y = 3.3, `0.6/(3x - 2y) = -1, 3x - 2y ≠ 0`
Solve the following pair of equations:
`4x + 6/y = 15, 6x - 8/y = 14, y ≠ 0`
Find the solution of the pair of equations `x/10 + y/5 - 1` = 0 and `x/8 + y/6` = 15. Hence, find λ, if y = λx + 5.
A shopkeeper sells a saree at 8% profit and a sweater at 10% discount, thereby, getting a sum Rs 1008. If she had sold the saree at 10% profit and the sweater at 8% discount, she would have got Rs 1028. Find the cost price of the saree and the list price (price before discount) of the sweater.
Vijay had some bananas, and he divided them into two lots A and B. He sold the first lot at the rate of Rs 2 for 3 bananas and the second lot at the rate of Re 1 per banana, and got a total of Rs 400. If he had sold the first lot at the rate of Re 1 per banana, and the second lot at the rate of Rs 4 for 5 bananas, his total collection would have been Rs 460. Find the total number of bananas he had.
