Advertisements
Advertisements
प्रश्न
उत्तर
We have,
\[\frac{dy}{dx} + 2y = 4x . . . . . \left( 1 \right)\]
Clearly, it is a linear differential equation of the form
\[\frac{dy}{dx} + Py = Q\]
where
\[P = 2 \]
\[Q = 4x \]
\[ \therefore \text{I.F.} = e^{\int P\ dx} \]
\[ = e^{\int2 dx} \]
\[ = e^{2x} \]
\[\text{ Multiplying both sides of } \left( 1 \right)\text{ by }e^{2x} ,\text{ we get }\]
\[ e^{2x} \left( \frac{dy}{dx} + 2y \right) = e^{2x} 4x \]
\[ \Rightarrow e^{2x} \frac{dy}{dx} + 2 e^{2x} y = e^{2x} 4x \]
Integrating both sides with respect to x, we get
\[y e^{2x} = 4\int x e^{2x} dx + C\]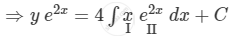
\[ \Rightarrow y e^{2x} = 4x\int e^{2x} dx - 4\int\left[ \frac{d}{dx}\left( x \right)\int e^{2x} dx \right]dx + C\]
\[ \Rightarrow y e^{2x} = 4x\frac{e^{2x}}{2} - 4 \times \frac{1}{2}\int e^{2x} dx + C\]
\[ \Rightarrow y e^{2x} = 2x e^{2x} - 4 \times \frac{1}{4} e^{2x} + C\]
\[ \Rightarrow y e^{2x} = 2x e^{2x} - e^{2x} + C\]
\[ \Rightarrow y e^{2x} = \left( 2x - 1 \right) e^{2x} + C\]
\[ \Rightarrow y = \left( 2x - 1 \right) + C e^{- 2x} \]
\[\text{ Hence, }y = \left( 2x - 1 \right) + C e^{- 2x}\text{ is the required solution.}\]
APPEARS IN
संबंधित प्रश्न
Find the integrating factor of the differential equation.
`((e^(-2^sqrtx))/sqrtx-y/sqrtx)dy/dx=1`
\[\frac{dy}{dx}\] + y cot x = x2 cot x + 2x
Experiments show that radium disintegrates at a rate proportional to the amount of radium present at the moment. Its half-life is 1590 years. What percentage will disappear in one year?
Solve the differential equation: (1 + x2) dy + 2xy dx = cot x dx
`("e"^(-2sqrt(x))/sqrt(x) - y/sqrt(x))("d"x)/("d"y) = 1(x ≠ 0)` when written in the form `"dy"/"dx" + "P"y` = Q, then P = ______.
`"dy"/"dx" + y` = 5 is a differential equation of the type `"dy"/"dx" + "P"y` = Q but it can be solved using variable separable method also.
Integrating factor of the differential equation of the form `("d"x)/("d"y) + "P"_1x = "Q"_1` is given by `"e"^(int P_1dy)`.
Solution of the differential equation of the type `("d"x)/("d"y) + "p"_1x = "Q"_1` is given by x.I.F. = `("I"."F") xx "Q"_1"d"y`.
Correct substitution for the solution of the differential equation of the type `("d"y)/("d"x) = "f"(x, y)`, where f(x, y) is a homogeneous function of zero degree is y = vx.
Correct substitution for the solution of the differential equation of the type `("d"x)/("d"y) = "g"(x, y)` where g(x, y) is a homogeneous function of the degree zero is x = vy.
Polio drops are delivered to 50 K children in a district. The rate at which polio drops are given is directly proportional to the number of children who have not been administered the drops. By the end of 2nd week half the children have been given the polio drops. How many will have been given the drops by the end of 3rd week can be estimated using the solution to the differential equation `"dy"/"dx" = "k"(50 - "y")` where x denotes the number of weeks and y the number of children who have been given the drops.
The solution of the differential equation `"dy"/"dx" = "k"(50 - "y")` is given by ______.
Polio drops are delivered to 50 K children in a district. The rate at which polio drops are given is directly proportional to the number of children who have not been administered the drops. By the end of 2nd week half the children have been given the polio drops. How many will have been given the drops by the end of 3rd week can be estimated using the solution to the differential equation `"dy"/"dx" = "k"(50 - "y")` where x denotes the number of weeks and y the number of children who have been given the drops.
Which of the following solutions may be used to find the number of children who have been given the polio drops?
The solution of the differential equation `(dx)/(dy) + Px = Q` where P and Q are constants or functions of y, is given by
If α, β are different values of x satisfying the equation a cos x + b sinα x = c, where a, b and c are constants, then `tan ((alpha + beta)/2)` is
Solve the differential equation: xdy – ydx = `sqrt(x^2 + y^2)dx`
Solve the following differential equation: (y – sin2x)dx + tanx dy = 0
If y = y(x) is the solution of the differential equation `(1 + e^(2x))(dy)/(dx) + 2(1 + y^2)e^x` = 0 and y(0) = 0, then `6(y^'(0) + (y(log_esqrt(3))))^2` is equal to ______.
The population P = P(t) at time 't' of a certain species follows the differential equation `("dp")/("dt")` = 0.5P – 450. If P(0) = 850, then the time at which population becomes zero is ______.
Let y = y(x) be the solution of the differential equation `e^xsqrt(1 - y^2)dx + (y/x)dy` = 0, y(1) = –1. Then, the value of (y(3))2 is equal to ______.
Let y = y(x) be the solution of the differential equation, `(x^2 + 1)^2 ("dy")/("d"x) + 2x(x^2 + 1)"y"` = 1, such that y(0) = 0. If `sqrt("ay")(1) = π/32` then the value of 'a' is ______.
The solution of the differential equation `(1 + y^2) + (x - e^(tan^-1y)) (dy)/(dx)` = 0, is ______.
Solve the differential equation:
`dy/dx` = cosec y
