Question

\[\frac{dy}{dx} + 2y = 4x\]

Answer 1

We have, 
\[\frac{dy}{dx} + 2y = 4x . . . . . \left( 1 \right)\]
Clearly, it is a linear differential equation of the form
\[\frac{dy}{dx} + Py = Q\]
where
\[P = 2 \]
\[Q = 4x \]
\[ \therefore \text{I.F.} = e^{\int P\ dx} \]
\[ = e^{\int2 dx} \]
\[ = e^{2x} \]
\[\text{ Multiplying both sides of } \left( 1 \right)\text{ by }e^{2x} ,\text{ we get }\]
\[ e^{2x} \left( \frac{dy}{dx} + 2y \right) = e^{2x} 4x \]
\[ \Rightarrow e^{2x} \frac{dy}{dx} + 2 e^{2x} y = e^{2x} 4x \]
Integrating both sides with respect to x, we get
\[y e^{2x} = 4\int x e^{2x} dx + C\]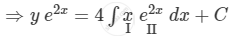

\[ \Rightarrow y e^{2x} = 4x\int e^{2x} dx - 4\int\left[ \frac{d}{dx}\left( x \right)\int e^{2x} dx \right]dx + C\]
\[ \Rightarrow y e^{2x} = 4x\frac{e^{2x}}{2} - 4 \times \frac{1}{2}\int e^{2x} dx + C\]
\[ \Rightarrow y e^{2x} = 2x e^{2x} - 4 \times \frac{1}{4} e^{2x} + C\]
\[ \Rightarrow y e^{2x} = 2x e^{2x} - e^{2x} + C\]
\[ \Rightarrow y e^{2x} = \left( 2x - 1 \right) e^{2x} + C\]
\[ \Rightarrow y = \left( 2x - 1 \right) + C e^{- 2x} \]
\[\text{ Hence, }y = \left( 2x - 1 \right) + C e^{- 2x}\text{ is the required solution.}\]