Question

Find the equation of the curve passing through the point (0, 2) given that the sum of the coordinates of any point on the curve exceeds the magnitude of the slope of the tangent to the curve at that point by 5.

Answer 1

According to the question,

\[\frac{dy}{dx} + 5 = x + y\]

\[\Rightarrow \frac{dy}{dx} - y = x - 5\]
\[\text{ Comparing with }\frac{dy}{dx} + Py = Q, \text{ we get }\]
\[P = - 1 \]
\[Q = x - 5\]
Now,
\[\text{ I . F . }= e^{- \int dx} = e^{- x} \]
So, the solution is given by
\[y \times I . F . = \int Q \times I . F . dx + C\]
\[ \Rightarrow y e^{- x} = \int\left( x - 5 \right) e^{- x} dx + C\]

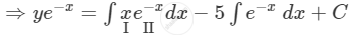
\[ \Rightarrow y e^{- x} = x\int e^{- x} dx - \int\left[ \frac{d}{dx}\left( x \right)\int e^{- x} dx \right]dx + 5 e^{- x} + C\]
\[ \Rightarrow y e^{- x} = - x e^{- x} + \int e^{- x} dx + 5 e^{- x} + C\]
\[ \Rightarrow y e^{- x} = - x e^{- x} - e^{- x} + 5 e^{- x} + C\]
\[ \Rightarrow y e^{- x} = - x e^{- x} + 4 e^{- x} + C\]
Since the curve passes throught the point 0, 2, it satisfies the equation of the curve.
\[2 e^0 = - 0 e^0 + 4 e^0 + C\]
\[ \Rightarrow C = - 2\]
Putting the value of C in the equation of the curve, we get
\[y e^{- x} = - x e^{- x} + 4 e^{- x} - 2\]
\[ \Rightarrow y = - x + 4 - 2 e^x \]
\[ \Rightarrow y = 4 - x - 2 e^x\]