Question

\[x\frac{dy}{dx} + y = x e^x\]

Answer 1

We have, 
\[x\frac{dy}{dx} + y = x e^x \]
\[ \Rightarrow \frac{dy}{dx} + \frac{1}{x}y = e^x . . . . . \left( 1 \right)\]
Clearly, it is a linear differential equation of the form
\[\frac{dy}{dx} + Py = Q\]
where
\[P = \frac{1}{x} \]
\[Q = e^x \]
\[ \therefore \text{I.F.} = e^{\int P\ dx} \]
\[ = e^{\int\frac{1}{x} dx} \]
\[ = e^{log x} \]
\[ = x \]
\[\text{Multiplying both sides of  }\left( 1 \right)\text{ by }x,\text{ we get }\]
\[x\left( \frac{dy}{dx} + \frac{1}{x}y \right) = x e^x \]
\[ \Rightarrow x\frac{dy}{dx} + y = x e^x \]
Integrating both sides with respect to x, we get
\[xy = \int x e^x dx + C\]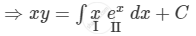

\[ \Rightarrow xy = x\int e^x dx - \int\left( \frac{d}{dx}\left( x \right)\int e^x dx \right)dx + C\]
\[ \Rightarrow xy = x e^x - e^x + C\]
\[ \Rightarrow xy = \left( x - 1 \right) e^x + C\]
\[ \Rightarrow y = \left( \frac{x - 1}{x} \right) e^x + \frac{C}{x}\]
\[\text{ Hence, }y = \left( \frac{x - 1}{x} \right) e^x + \frac{C}{x}\text{ is the required solution.}\]