Advertisements
Advertisements
प्रश्न
उत्तर
We have,
\[x\frac{dy}{dx} + y = x e^x \]
\[ \Rightarrow \frac{dy}{dx} + \frac{1}{x}y = e^x . . . . . \left( 1 \right)\]
Clearly, it is a linear differential equation of the form
\[\frac{dy}{dx} + Py = Q\]
where
\[P = \frac{1}{x} \]
\[Q = e^x \]
\[ \therefore \text{I.F.} = e^{\int P\ dx} \]
\[ = e^{\int\frac{1}{x} dx} \]
\[ = e^{log x} \]
\[ = x \]
\[\text{Multiplying both sides of }\left( 1 \right)\text{ by }x,\text{ we get }\]
\[x\left( \frac{dy}{dx} + \frac{1}{x}y \right) = x e^x \]
\[ \Rightarrow x\frac{dy}{dx} + y = x e^x \]
Integrating both sides with respect to x, we get
\[xy = \int x e^x dx + C\]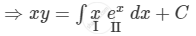
\[ \Rightarrow xy = x\int e^x dx - \int\left( \frac{d}{dx}\left( x \right)\int e^x dx \right)dx + C\]
\[ \Rightarrow xy = x e^x - e^x + C\]
\[ \Rightarrow xy = \left( x - 1 \right) e^x + C\]
\[ \Rightarrow y = \left( \frac{x - 1}{x} \right) e^x + \frac{C}{x}\]
\[\text{ Hence, }y = \left( \frac{x - 1}{x} \right) e^x + \frac{C}{x}\text{ is the required solution.}\]
APPEARS IN
संबंधित प्रश्न
Solve the differential equation ` (1 + x2) dy/dx+y=e^(tan^(−1))x.`
Solve `sin x dy/dx - y = sin x.tan x/2`
\[\frac{dy}{dx}\] = y tan x − 2 sin x
\[\frac{dy}{dx}\] + y tan x = cos x
\[\frac{dy}{dx}\] + y cot x = x2 cot x + 2x
The decay rate of radium at any time t is proportional to its mass at that time. Find the time when the mass will be halved of its initial mass.
Experiments show that radium disintegrates at a rate proportional to the amount of radium present at the moment. Its half-life is 1590 years. What percentage will disappear in one year?
A wet porous substance in the open air loses its moisture at a rate proportional to the moisture content. If a sheet hung in the wind loses half of its moisture during the first hour, when will it have lost 95% moisture, weather conditions remaining the same.
Solve the differential equation : `"x"(d"y")/(d"x") + "y" - "x" + "xy"cot"x" = 0; "x" != 0.`
`("e"^(-2sqrt(x))/sqrt(x) - y/sqrt(x))("d"x)/("d"y) = 1(x ≠ 0)` when written in the form `"dy"/"dx" + "P"y` = Q, then P = ______.
`"dy"/"dx" + y` = 5 is a differential equation of the type `"dy"/"dx" + "P"y` = Q but it can be solved using variable separable method also.
`("d"y)/("d"x) + y/(xlogx) = 1/x` is an equation of the type ______.
Correct substitution for the solution of the differential equation of the type `("d"y)/("d"x) = "f"(x, y)`, where f(x, y) is a homogeneous function of zero degree is y = vx.
Solve the differential equation:
`"dy"/"dx" = 2^(-"y")`
The solution of the differential equation `(dx)/(dy) + Px = Q` where P and Q are constants or functions of y, is given by
The solution of the differential equation `(dy)/(dx) = 1 + x + y + xy` when y = 0 at x = – 1 is
Form the differential equation of the family of parabolas having vertex at origin and axis along positive y-axis.
Solve the differential equation: xdy – ydx = `sqrt(x^2 + y^2)dx`
Let y = y(x) be the solution of the differential equation `(dy)/(dx) + (sqrt(2)y)/(2cos^4x - cos2x) = xe^(tan^-1(sqrt(2)cost2x)), 0 < x < π/2` with `y(π/4) = π^2/32`. If `y(π/3) = π^2/18e^(-tan^-1(α))`, then the value of 3α2 is equal to ______.
If y = y(x) is the solution of the differential equation `(1 + e^(2x))(dy)/(dx) + 2(1 + y^2)e^x` = 0 and y(0) = 0, then `6(y^'(0) + (y(log_esqrt(3))))^2` is equal to ______.
The population P = P(t) at time 't' of a certain species follows the differential equation `("dp")/("dt")` = 0.5P – 450. If P(0) = 850, then the time at which population becomes zero is ______.
Let y = y(x) be the solution of the differential equation `xtan(y/x)dy = (ytan(y/x) - x)dx, -1 ≤ x ≤ 1, y(1/2) = π/6`. Then the area of the region bounded by the curves x = 0, x = `1/sqrt(2)` and y = y(x) in the upper half plane is ______.
The solution of the differential equation `(1 + y^2) + (x - e^(tan^-1y)) (dy)/(dx)` = 0, is ______.
