Advertisements
Advertisements
Question
Solution
We have,
\[x\frac{dy}{dx} + y = x \log x\]
Dividing both sides by x, we get
\[\frac{dy}{dx} + \frac{y}{x} = \log x\]
\[\text{ Comparing with }\frac{dy}{dx} + Py = Q,\text{ we get }\]
\[P = \frac{1}{x}\]
\[Q = \log x\]
Now,
\[\text{I.F.} = e^{\int P\ dx} = e^{\int\frac{1}{x}dx} \]
\[ = e^{log\left| x \right|} \]
\[ = x\]
So, the solution is given by
\[y \times \text{I.F.} = \int Q \times \text{I.F.} dx + C\]
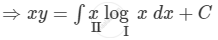
\[ \Rightarrow xy = \log x\int xdx - \int\left[ \frac{d}{dx}\left( \log x \right)\int x dx \right]dx + C\]
\[ \Rightarrow xy = \frac{x^2 \log x}{2} - \int\frac{x}{2}dx + C\]
\[ \Rightarrow xy = \frac{x^2 \log x}{2} - \frac{x^2}{4} + C\]
\[ \Rightarrow 4xy = 2 x^2 \log x - x^2 + K ..........\left(\text{where, }K = 2C \right)\]
APPEARS IN
RELATED QUESTIONS
Solve the following differential equation: `(x^2-1)dy/dx+2xy=2/(x^2-1)`
Find the integrating factor for the following differential equation:`x logx dy/dx+y=2log x`
Solve the differential equation ` (1 + x2) dy/dx+y=e^(tan^(−1))x.`
\[\frac{dy}{dx}\] + y cot x = x2 cot x + 2x
The slope of the tangent to the curve at any point is the reciprocal of twice the ordinate at that point. The curve passes through the point (4, 3). Determine its equation.
The decay rate of radium at any time t is proportional to its mass at that time. Find the time when the mass will be halved of its initial mass.
Experiments show that radium disintegrates at a rate proportional to the amount of radium present at the moment. Its half-life is 1590 years. What percentage will disappear in one year?
Solve the differential equation: (1 + x2) dy + 2xy dx = cot x dx
`("e"^(-2sqrt(x))/sqrt(x) - y/sqrt(x))("d"x)/("d"y) = 1(x ≠ 0)` when written in the form `"dy"/"dx" + "P"y` = Q, then P = ______.
Correct substitution for the solution of the differential equation of the type `("d"x)/("d"y) = "g"(x, y)` where g(x, y) is a homogeneous function of the degree zero is x = vy.
If ex + ey = ex+y, then `"dy"/"dx"` is:
Polio drops are delivered to 50 K children in a district. The rate at which polio drops are given is directly proportional to the number of children who have not been administered the drops. By the end of 2nd week half the children have been given the polio drops. How many will have been given the drops by the end of 3rd week can be estimated using the solution to the differential equation `"dy"/"dx" = "k"(50 - "y")` where x denotes the number of weeks and y the number of children who have been given the drops.
The solution of the differential equation `"dy"/"dx" = "k"(50 - "y")` is given by ______.
Solve the differential equation:
`"dy"/"dx" = 2^(-"y")`
The solution of the differential equation `(dx)/(dy) + Px = Q` where P and Q are constants or functions of y, is given by
If α, β are different values of x satisfying the equation a cos x + b sinα x = c, where a, b and c are constants, then `tan ((alpha + beta)/2)` is
The solution of the differential equation `(dy)/(dx) = 1 + x + y + xy` when y = 0 at x = – 1 is
`int cos(log x) dx = F(x) + C` where C is arbitrary constant. Here F(x) =
If `x (dy)/(dx) = y(log y - log x + 1)`, then the solution of the dx equation is
Solve the following differential equation: (y – sin2x)dx + tanx dy = 0
If y = y(x) is the solution of the differential equation `(1 + e^(2x))(dy)/(dx) + 2(1 + y^2)e^x` = 0 and y(0) = 0, then `6(y^'(0) + (y(log_esqrt(3))))^2` is equal to ______.
The population P = P(t) at time 't' of a certain species follows the differential equation `("dp")/("dt")` = 0.5P – 450. If P(0) = 850, then the time at which population becomes zero is ______.
Let y = y(x) be the solution of the differential equation, `(2 + sinxdy)/(y + 1) (dy)/(dx)` = –cosx. If y > 0, y(0) = 1. If y(π) = a, and `(dy)/(dx)` at x = π is b, then the ordered pair (a, b) is equal to ______.
If y = f(x), f'(0) = f(0) = 1 and if y = f(x) satisfies `(d^2y)/(dx^2) + (dy)/(dx)` = x, then the value of [f(1)] is ______ (where [.] denotes greatest integer function)
Solve the differential equation:
`dy/dx` = cosec y
