Advertisements
Advertisements
प्रश्न
उत्तर
We have,
\[x\frac{dy}{dx} + y = x \log x\]
Dividing both sides by x, we get
\[\frac{dy}{dx} + \frac{y}{x} = \log x\]
\[\text{ Comparing with }\frac{dy}{dx} + Py = Q,\text{ we get }\]
\[P = \frac{1}{x}\]
\[Q = \log x\]
Now,
\[\text{I.F.} = e^{\int P\ dx} = e^{\int\frac{1}{x}dx} \]
\[ = e^{log\left| x \right|} \]
\[ = x\]
So, the solution is given by
\[y \times \text{I.F.} = \int Q \times \text{I.F.} dx + C\]
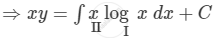
\[ \Rightarrow xy = \log x\int xdx - \int\left[ \frac{d}{dx}\left( \log x \right)\int x dx \right]dx + C\]
\[ \Rightarrow xy = \frac{x^2 \log x}{2} - \int\frac{x}{2}dx + C\]
\[ \Rightarrow xy = \frac{x^2 \log x}{2} - \frac{x^2}{4} + C\]
\[ \Rightarrow 4xy = 2 x^2 \log x - x^2 + K ..........\left(\text{where, }K = 2C \right)\]
APPEARS IN
संबंधित प्रश्न
Find the integrating factor for the following differential equation:`x logx dy/dx+y=2log x`
Find the integrating factor of the differential equation.
`((e^(-2^sqrtx))/sqrtx-y/sqrtx)dy/dx=1`
The slope of the tangent to the curve at any point is the reciprocal of twice the ordinate at that point. The curve passes through the point (4, 3). Determine its equation.
The decay rate of radium at any time t is proportional to its mass at that time. Find the time when the mass will be halved of its initial mass.
Solve the differential equation: (x + 1) dy – 2xy dx = 0
Solve the differential equation : `"x"(d"y")/(d"x") + "y" - "x" + "xy"cot"x" = 0; "x" != 0.`
Solve the following differential equation :
`"dy"/"dx" + "y" = cos"x" - sin"x"`
Solve the differential equation `"dy"/"dx" + y/x` = x2.
`("e"^(-2sqrt(x))/sqrt(x) - y/sqrt(x))("d"x)/("d"y) = 1(x ≠ 0)` when written in the form `"dy"/"dx" + "P"y` = Q, then P = ______.
Correct substitution for the solution of the differential equation of the type `("d"x)/("d"y) = "g"(x, y)` where g(x, y) is a homogeneous function of the degree zero is x = vy.
The solution of the differential equation `(dx)/(dy) + Px = Q` where P and Q are constants or functions of y, is given by
If α, β are different values of x satisfying the equation a cos x + b sinα x = c, where a, b and c are constants, then `tan ((alpha + beta)/2)` is
The solution of the differential equation `(dy)/(dx) = 1 + x + y + xy` when y = 0 at x = – 1 is
`int cos(log x) dx = F(x) + C` where C is arbitrary constant. Here F(x) =
If `x (dy)/(dx) = y(log y - log x + 1)`, then the solution of the dx equation is
Form the differential equation of the family of parabolas having vertex at origin and axis along positive y-axis.
Solve the differential equation: xdy – ydx = `sqrt(x^2 + y^2)dx`
Solve the following differential equation: (y – sin2x)dx + tanx dy = 0
Find the general solution of the differential equation: (x3 + y3)dy = x2ydx
Let y = y(x) be the solution of the differential equation `(dy)/(dx) + (sqrt(2)y)/(2cos^4x - cos2x) = xe^(tan^-1(sqrt(2)cost2x)), 0 < x < π/2` with `y(π/4) = π^2/32`. If `y(π/3) = π^2/18e^(-tan^-1(α))`, then the value of 3α2 is equal to ______.
The population P = P(t) at time 't' of a certain species follows the differential equation `("dp")/("dt")` = 0.5P – 450. If P(0) = 850, then the time at which population becomes zero is ______.
