Question

\[x\frac{dy}{dx} + y = x \log x\]

Answer 1

We have,
\[x\frac{dy}{dx} + y = x \log x\]
Dividing both sides by x, we get

\[\frac{dy}{dx} + \frac{y}{x} = \log x\]

\[\text{ Comparing with }\frac{dy}{dx} + Py = Q,\text{ we get }\]

\[P = \frac{1}{x}\]

\[Q = \log x\]

Now, 

\[\text{I.F.} = e^{\int P\ dx} = e^{\int\frac{1}{x}dx} \]

\[ = e^{log\left| x \right|} \]

\[ = x\]

So, the solution is given by

\[y \times \text{I.F.} = \int Q \times \text{I.F.} dx + C\]

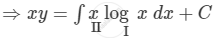
\[ \Rightarrow xy = \log x\int xdx - \int\left[ \frac{d}{dx}\left( \log x \right)\int x dx \right]dx + C\]

\[ \Rightarrow xy = \frac{x^2 \log x}{2} - \int\frac{x}{2}dx + C\]

\[ \Rightarrow xy = \frac{x^2 \log x}{2} - \frac{x^2}{4} + C\]

\[ \Rightarrow 4xy = 2 x^2 \log x - x^2 + K ..........\left(\text{where, }K = 2C \right)\]