Question

Explain in detail the isochoric process.

Answer 1

Isochoric process: This is a thermodynamic process in which the volume of the system is kept constant. But pressure, temperature and internal energy continue to be variables.

The pressure-volume graph for an isochoric process is a vertical line parallel to the pressure axis as shown in Figure.

Isochoric process with increased pressure

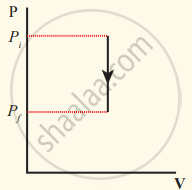
Isochoric process with decreased pressure

           Isochoric process

P = `((μ"R")/"V")"T"` ...............(1)

where `((μ"R")/"V")` = constant

We can infer that the pressure is directly proportional to temperature. This implies that the P-T graph for an isochoric process is a straight line passing through the origin. If gas goes from the state (P_i, T_i) to (P_f, T_f) at constant volume, then the system satisfies the following equation

`"P"_"i"/"T"_"i" = "P"_"f"/"T"_"f"` .....,,,(2)

For an isochoric processes, ∆V = 0 and W = 0. Then the first law becomes

∆U = 0 .................(3)

Implying that the heat supplied is used to increase only the internal energy. As a result the temperature increases and pressure also increases.

Suppose a system loses heat to the surroundings through conducting walls by keeping the volume constant, then its internal energy decreases. As a result the temperature decreases; the pressure also decreases.