Advertisements
Advertisements
प्रश्न
Find the distance between the points \[\left( - \frac{8}{5}, 2 \right)\] and \[\left( \frac{2}{5}, 2 \right)\] .
उत्तर
We have to find the distance between `A ( - 8/5, 2)" and " B ( 2/5 , 2) `.
In general, the distance between A`(x_1, y_1) " and B "(x_2 , y_2) ` is given by,
`AB = sqrt((x_2 - x_1 )^2 + (y_2 - y_1)^2)`
So,
`AB = sqrt((2/5 + 8/5)^2 + (2-2)^2)`
` = sqrt(4) `
= 2
APPEARS IN
संबंधित प्रश्न
Prove that the points (−2, 5), (0, 1) and (2, −3) are collinear.
Show that the points (−3, 2), (−5,−5), (2, −3) and (4, 4) are the vertices of a rhombus. Find the area of this rhombus.
In what ratio is the line segment joining (-3, -1) and (-8, -9) divided at the point (-5, -21/5)?
Show that the following points are the vertices of a square:
(i) A (3,2), B(0,5), C(-3,2) and D(0,-1)
In what ratio does the line x - y - 2 = 0 divide the line segment joining the points A (3, 1) and B (8, 9)?
ΔXYZ ∼ ΔPYR; In ΔXYZ, ∠Y = 60o, XY = 4.5 cm, YZ = 5.1 cm and XYPY =` 4/7` Construct ΔXYZ and ΔPYR.
A point whose abscissa is −3 and ordinate 2 lies in
Prove hat the points A (2, 3) B(−2,2) C(−1,−2), and D(3, −1) are the vertices of a square ABCD.
Find the value of k, if the points A(7, −2), B (5, 1) and C (3, 2k) are collinear.
Write the ratio in which the line segment doining the points A (3, −6), and B (5, 3) is divided by X-axis.
If points (t, 2t), (−2, 6) and (3, 1) are collinear, then t =
If the centroid of a triangle is (1, 4) and two of its vertices are (4, −3) and (−9, 7), then the area of the triangle is
Write the equations of the x-axis and y-axis.
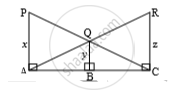
In the above figure, seg PA, seg QB and RC are perpendicular to seg AC. From the information given in the figure, prove that: `1/x + 1/y = 1/z`
What are the coordinates of origin?
Point P(– 4, 2) lies on the line segment joining the points A(– 4, 6) and B(– 4, – 6).
Which of the points P(0, 3), Q(1, 0), R(0, –1), S(–5, 0), T(1, 2) do not lie on the x-axis?
Find the coordinates of the point which lies on x and y axes both.
Find the coordinates of the point whose abscissa is 5 and which lies on x-axis.
Assertion (A): The ratio in which the line segment joining (2, -3) and (5, 6) internally divided by x-axis is 1:2.
Reason (R): as formula for the internal division is `((mx_2 + nx_1)/(m + n) , (my_2 + ny_1)/(m + n))`
