Advertisements
Advertisements
प्रश्न
Find fog and gof if : f(x) = c, c ∈ R, g(x) = sin `x^2`
उत्तर
f (x) = c, g (x) = sin x2
f : R → {c} ; g : R→ [ 0, 1 ]
Computing fog :
Clearly, the range of g is a subset of the domain of f.
fog : R→R
(fog) (x) = f (g (x))
= f (sin x2)
= c
Computing gof :
Clearly, the range of f is a subset of the domain of g.
⇒ fog : R→ R
(gof) (x) = g (f (x))
= g (c)
= sin c2
APPEARS IN
संबंधित प्रश्न
Check the injectivity and surjectivity of the following function:
f: R → R given by f(x) = x2
Give an example of a function which is neither one-one nor onto ?
Classify the following function as injection, surjection or bijection : f : N → N given by f(x) = x2
Show that the function f : R − {3} → R − {2} given by f(x) = `(x-2)/(x-3)` is a bijection.
Find the number of all onto functions from the set A = {1, 2, 3, ..., n} to itself.
Find gof and fog when f : R → R and g : R → R is defined by f(x) = 2x + 3 and g(x) = x2 + 5 .
Find fog (2) and gof (1) when : f : R → R ; f(x) = x2 + 8 and g : R → R; g(x) = 3x3 + 1.
if f (x) = `sqrt (x +3) and g (x) = x ^2 + 1` be two real functions, then find fog and gof.
State with reason whether the following functions have inverse:
h : {2, 3, 4, 5} → {7, 9, 11, 13} with h = {(2, 7), (3, 9), (4, 11), (5, 13)}
Let A = {x &epsis; R | −1 ≤ x ≤ 1} and let f : A → A, g : A → A be two functions defined by f(x) = x2 and g(x) = sin (π x/2). Show that g−1 exists but f−1 does not exist. Also, find g−1.
Let \[f : \left[ - \frac{\pi}{2}, \frac{\pi}{2} \right] \to\] A be defined by f(x) = sin x. If f is a bijection, write set A.
If f : R → R is defined by f(x) = 3x + 2, find f (f (x)).
Let A = {1, 2, 3}, B = {4, 5, 6, 7} and let f = {(1, 4), (2, 5), (3, 6)} be a function from A to B. State whether f is one-one or not.
\[f : R \to R \text{given by} f\left( x \right) = x + \sqrt{x^2} \text{ is }\]
Which of the following functions form Z to itself are bijections?
Which of the following functions from
to itself are bijections?
If a function\[f : [2, \infty )\text{ to B defined by f}\left( x \right) = x^2 - 4x + 5\] is a bijection, then B =
The function
\[f : R \to R\] defined by\[f\left( x \right) = \left( x - 1 \right) \left( x - 2 \right) \left( x - 3 \right)\]
(a) one-one but not onto
(b) onto but not one-one
(c) both one and onto
(d) neither one-one nor onto
Let
\[f : [2, \infty ) \to X\] be defined by
\[f\left( x \right) = 4x - x^2\] Then, f is invertible if X =
Let f: R → R be the function defined by f(x) = 4x – 3 ∀ x ∈ R. Then write f–1
Let f: R → R be defined by f(x) = 3x – 4. Then f–1(x) is given by ______.
Let A be a finite set. Then, each injective function from A into itself is not surjective.
For sets A, B and C, let f: A → B, g: B → C be functions such that g o f is injective. Then both f and g are injective functions.
If f: R → R is defined by f(x) = x2 – 3x + 2, write f(f (x))
If the set A contains 5 elements and the set B contains 6 elements, then the number of one-one and onto mappings from A to B is ______.
Let f: R – `{3/5}` → R be defined by f(x) = `(3x + 2)/(5x - 3)`. Then ______.
Let f: R → R be given by f(x) = tan x. Then f–1(1) is ______.
Let g(x) = x2 – 4x – 5, then ____________.
Let f : [0, ∞) → [0, 2] be defined by `"f" ("x") = (2"x")/(1 + "x"),` then f is ____________.
A general election of Lok Sabha is a gigantic exercise. About 911 million people were eligible to vote and voter turnout was about 67%, the highest ever

Let I be the set of all citizens of India who were eligible to exercise their voting right in the general election held in 2019. A relation ‘R’ is defined on I as follows:
R = {(V1, V2) ∶ V1, V2 ∈ I and both use their voting right in the general election - 2019}
- Three friends F1, F2, and F3 exercised their voting right in general election-2019, then which of the following is true?
Students of Grade 9, planned to plant saplings along straight lines, parallel to each other to one side of the playground ensuring that they had enough play area. Let us assume that they planted one of the rows of the saplings along the line y = x − 4. Let L be the set of all lines which are parallel on the ground and R be a relation on L.
Answer the following using the above information.
- The function f: R → R defined by f(x) = x − 4 is ____________.
Students of Grade 9, planned to plant saplings along straight lines, parallel to each other to one side of the playground ensuring that they had enough play area. Let us assume that they planted one of the rows of the saplings along the line y = x − 4. Let L be the set of all lines which are parallel on the ground and R be a relation on L.
Answer the following using the above information.
- Let f: R → R be defined by f(x) = x − 4. Then the range of f(x) is ____________.
Raji visited the Exhibition along with her family. The Exhibition had a huge swing, which attracted many children. Raji found that the swing traced the path of a Parabola as given by y = x2.
Answer the following questions using the above information.
- The function f: Z → Z defined by f(x) = x2 is ____________.
If f; R → R f(x) = 10x + 3 then f–1(x) is:
Number of integral values of x satisfying the inequality `(3/4)^(6x + 10 - x^2) < 27/64` is ______.
Let x is a real number such that are functions involved are well defined then the value of `lim_(t→0)[max{(sin^-1 x/3 + cos^-1 x/3)^2, min(x^2 + 4x + 7)}]((sin^-1t)/t)` where [.] is greatest integer function and all other brackets are usual brackets.
Which one of the following graphs is a function of x?
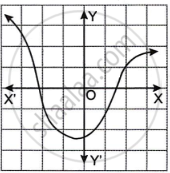 |
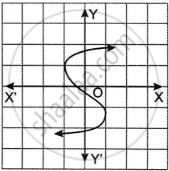 |
| Graph A | Graph B |
