Advertisements
Advertisements
प्रश्न
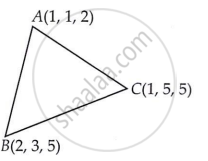
Find the area of the triangle with vertices A (1, 1, 2), B (2, 3, 5) and C (1, 5, 5).
उत्तर
Here,
`vec (BC) = (hati + 5hatj + 5hatk) - (2hati + 3hatj + 5hatk)`
`= -hati + 2hatj`
`vec(BA) = (hati + hatj + 2hatk) - (2hati + 3hatj + 5hatk)`
`= -hati - 2hatj - 3hatk`
∴ `vec(BC) xxvec (BA) = abs((hati, hatj, hatk), (-1, 2, 0), (-1, -2, -3))`
`= (-6 + 0)hati - (3 + 0)hatj + (2 + 2)hatk`
`= -6hati - 3hatj + 4hatk`
So, `|vec(BC) xx vec( BA)| = sqrt(36 + 9 + 16)`
`= sqrt61`
∴ Area of `triangle ABC = 1/2 |vec(BC) xx vec(BA)|`
`= 1/2 (sqrt61)` sq. units.
APPEARS IN
संबंधित प्रश्न
If `veca = 2hati + 2hatj + 3hatk, vecb = -veci + 2hatj + hatk and vecc = 3hati + hatj` are such that `veca + lambdavecb` is perpendicular to `vecc`, then find the value of λ.
Find `|veca × vecb|`, if `veca = hati - 7hatj + 7hatk` and `vecb = 3hati - 2hatj + 2hatk`.
Given that `veca.vecb = 0` and `veca xx vecb = 0` What can you conclude about the vectors `veca and vecb`?
Let the vectors `veca, vecb, vecc` given as `a_1hati + a_2hatj + a_3hatk, b_1hati + b_2hatj + b_3hatk, c_1hati + c_2hatj + c_3hatk` Then show that = `veca xx (vecb+ vecc) = veca xx vecb + veca xx vecc.`
If either `veca = vec0` or `vecb = vec0`, then `veca xxvecb = vec0`. Is the converse true? Justify your answer with an example.
Area of a rectangle having vertices A, B, C, and D with position vectors `-hati + 1/2 hatj + 4hatk, hati + 1/2 hatj + 4hatk, and -hati - 1/2j + 4hatk,` respectively is ______.
Find a unit vector perpendicular to the plane containing the vectors \[\vec{a} = 2 \hat{ i } + \hat{ j } + \hat{ k } \text{ and } \vec{b} = \hat{ i } + 2 \hat{ j } + \hat{ k } .\]
Find the area of the parallelogram determined by the vector \[3 \hat{ i } + \hat{ j } - 2 \hat{ k } \text{ and } \hat{ i } - 3 \hat{ j } + 4 \hat{ k } \] .
Find the area of the parallelogram determined by the vector \[\hat{ i } - 3 \hat{ j } + \hat{ k } \text{ and } \hat{ i } + \hat{ j } + \hat{ k } .\]
If \[\vec{a} = 2 \hat{ i } + 5 \hat{ j } - 7 \hat{ k } , \vec{b} = - 3 \hat{ i } + 4 \hat{ j } + \hat{ k } \text{ and } \vec{c} = \hat{ i } - 2 \hat{ j } - 3 \hat{ k } ,\] compute \[\left( \vec{a} \times \vec{b} \right) \times \vec{c} \text{ and } \vec{a} \times \left( \vec{b} \times \vec{c} \right)\] and verify that these are not equal.
What inference can you draw if \[\vec{a} \times \vec{b} = \vec{0} \text{ and } \vec{a} \cdot \vec{b} = 0 .\]
if \[\vec{a} = \hat{ i }- 2\hat{ j } + 3 \hat{ k } , \text{ and } \vec{b} = 2 \hat{ i } + 3 \hat{ j } - 5 \hat{ k } ,\] then find \[\vec{a} \times \vec{b} .\] Verify th at \[\vec{a} \text{ and } \vec{a} \times \vec{b}\] are perpendicular to each other.
If \[\vec{p} \text{ and } \vec{q}\] are unit vectors forming an angle of 30°; find the area of the parallelogram having \[\vec{a} = \vec{p} + 2 \vec{q} \text{ and } \vec{b} = 2 \vec{p} + \vec{q}\] as its diagonals.
Let \[\vec{a} = \hat{ i } + 4 \hat{ j } + 2 \hat{ k } , \vec{b} = 3 \hat{ i }- 2 \hat{ j } + 7 \hat{ k } \text{ and } \vec{c} = 2 \hat{ i } - \hat{ j } + 4 \hat{ k } .\] Find a vector \[\vec{d}\] which is perpendicular to both \[\vec{a} \text{ and } \vec{d}\] \[\text{ and } \vec{c} \cdot \vec{d} = 15 .\]
If \[\vec{a} = 2 \hat{ i } - 3 \hat{ j } + \hat{ k } , \vec{b} = -\hat{ i } + \hat{ k } , \vec{c} = 2 \hat{ j } - \hat{ k } \] are three vectors, find the area of the parallelogram having diagonals \[\left( \vec{a} + \vec{b} \right)\] and \[\left( \vec{b} + \vec{c} \right)\] .
Define vector product of two vectors.
Write the value \[\left( \hat{ i } \times \hat{ j } \right) \cdot \hat{ k } + \hat{ i } \cdot \hat{ j } .\]
Write the value of \[\hat{ i } . \left( \hat{ j } \times \hat{ k } \right) + \hat{ j } . \left( \hat{ k } \times \hat{ i } \right) + \hat{ k } . \left( \hat{ j } \times \hat{ i } \right) .\]
Write the value of \[\hat{ i } . \left( \hat{ j } \times \hat{ k } \right) + \hat{ j } . \left( \hat{ k } \times \hat{ i } \right) + \hat{ k } . \left( \hat{ i } \times \hat{ j } \right) .\]
Write the expression for the area of the parallelogram having \[\vec{a} \text{ and } \vec{b}\] as its diagonals.
For any two vectors \[\vec{a} \text{ and } \vec{b}\] write the value of \[\left( \vec{a} . \vec{b} \right)^2 + \left| \vec{a} \times \vec{b} \right|^2\] in terms of their magnitudes.
For any two vectors \[\vec{a}\] and \[\vec{b}\] , find \[\vec{a} . \left( \vec{b} \times \vec{a} \right) .\]
Write a unit vector perpendicular to \[\hat{ i } + \hat{ j } \text{ and } \hat{ j } + \hat{ k } .\]
If \[\left| \vec{a} \times \vec{b} \right|^2 + \left( \vec{a} . \vec{b} \right)^2 = 144\] and \[\left| \vec{a} \right| = 4,\] find \[\left| \vec{b} \right|\] .
If \[\vec{a} \text{ and } \vec{b}\] are unit vectors such that \[\vec{a} \times \vec{b}\] is also a unit vector, find the angle between \[\vec{a} \text{ and } \vec{b}\] .
Write the number of vectors of unit length perpendicular to both the vectors \[\vec{a} = 2 \hat{ i } + \hat{ j } + 2 \hat{ k } \text{ and } \vec{b} = \hat{ j } + \hat{ k } \] .
Write the angle between the vectors \[\vec{a} \times \vec{b}\] and \[\vec{b} \times \vec{a}\] .
The vector \[\vec{b} = 3 \hat { i }+ 4 \hat {k }\] is to be written as the sum of a vector \[\vec{\alpha}\] parallel to \[\vec{a} = \hat {i} + \hat {j}\] and a vector \[\vec{\beta}\] perpendicular to \[\vec{a}\]. Then \[\vec{\alpha} =\]
If \[\vec{a} = 2 \hat{ i } - 3 \hat{ j } - \hat{ k } \text{ and } \vec{b} = \hat{ i } + 4 \hat{ j } - 2 \hat{ k
} , \text{ then } \vec{a} \times \vec{b}\] is
The value of \[\left( \vec{a} \times \vec{b} \right)^2\] is
(a) If `veca = hati - 2j + 3veck , vecb = 2hati + 3hatj - 5hatk,` prove that `veca and vecaxxvecb` are perpendicular.
Let `veca = hati + hatj, vecb = hati - hatj` and `vecc = hati + hatj + hatk`. If `hatn` is a unit vector such that `veca.hatn` = 0 and `vecb.hatn` = 0, then find `|vecc.hatn|`.
If `veca` and `vecb` are unit vectors inclined at an angle 30° to each other, then find the area of the parallelogram with `(veca + 3vecb)` and `(3veca + vecb)` as adjacent sides.
The two adjacent sides of a parallelogram are represented by vectors `2hati - 4hatj + 5hatk` and `hati - 2hatj - 3hatk`. Find the unit vector parallel to one of its diagonals, Also, find the area of the parallelogram.
Let `veca = 2hati + hatj - 2hatk, vecb = hati + hatj`. If `vecc` is a vector such that `veca . vecc = \|vecc|, |vecc - veca| = 2sqrt(2)` and the angle between `veca xx vecb` and `vecc` is 30°, then `|(veca xx vecb) xx vecc|` equals ______.
If `veca = hati + hatj + hatk` and `vecb = hati + 2hatj + 3hatk` then find a unit vector perpendicular to both `veca + vecb` and `veca - vecb`.
If `veca` and `vecb` are two non-zero vectors such that `|veca xx vecb| = veca.vecb`, find the angle between `veca` and `vecb`.
If `veca` is a unit vector perpendicular to `vecb` and `(veca + 2vecb).(3veca - vecb) = -5`, find `|vecb|`.
