Topics
Relations and Functions
Relations and Functions
Inverse Trigonometric Functions
Algebra
Calculus
Matrices
- Introduction of Matrices
- Order of a Matrix
- Types of Matrices
- Equality of Matrices
- Introduction of Operations on Matrices
- Addition of Matrices
- Multiplication of a Matrix by a Scalar
- Properties of Matrix Addition
- Properties of Scalar Multiplication of a Matrix
- Multiplication of Matrices
- Properties of Multiplication of Matrices
- Transpose of a Matrix
- Properties of Transpose of the Matrices
- Symmetric and Skew Symmetric Matrices
- Invertible Matrices
- Inverse of a Matrix by Elementary Transformation
- Multiplication of Two Matrices
- Negative of Matrix
- Subtraction of Matrices
- Proof of the Uniqueness of Inverse
- Elementary Transformations
- Matrices Notation
Determinants
- Introduction of Determinant
- Determinants of Matrix of Order One and Two
- Determinant of a Matrix of Order 3 × 3
- Area of a Triangle
- Minors and Co-factors
- Inverse of a Square Matrix by the Adjoint Method
- Applications of Determinants and Matrices
- Elementary Transformations
- Properties of Determinants
- Determinant of a Square Matrix
- Rule A=KB
Vectors and Three-dimensional Geometry
Linear Programming
Continuity and Differentiability
- Concept of Continuity
- Algebra of Continuous Functions
- Concept of Differentiability
- Derivatives of Composite Functions - Chain Rule
- Derivatives of Implicit Functions
- Derivatives of Inverse Trigonometric Functions
- Exponential and Logarithmic Functions
- Logarithmic Differentiation
- Derivatives of Functions in Parametric Forms
- Second Order Derivative
- Derivative - Exponential and Log
- Proof Derivative X^n Sin Cos Tan
- Infinite Series
- Higher Order Derivative
- Continuous Function of Point
- Mean Value Theorem
Applications of Derivatives
- Introduction to Applications of Derivatives
- Rate of Change of Bodies or Quantities
- Increasing and Decreasing Functions
- Maxima and Minima
- Maximum and Minimum Values of a Function in a Closed Interval
- Simple Problems on Applications of Derivatives
- Graph of Maxima and Minima
- Approximations
- Tangents and Normals
Probability
Integrals
- Introduction of Integrals
- Integration as an Inverse Process of Differentiation
- Some Properties of Indefinite Integral
- Methods of Integration: Integration by Substitution
- Integration Using Trigonometric Identities
- Integrals of Some Particular Functions
- Methods of Integration: Integration Using Partial Fractions
- Methods of Integration: Integration by Parts
- Fundamental Theorem of Calculus
- Evaluation of Definite Integrals by Substitution
- Properties of Definite Integrals
- Definite Integrals
- Indefinite Integral Problems
- Comparison Between Differentiation and Integration
- Geometrical Interpretation of Indefinite Integrals
- Indefinite Integral by Inspection
- Definite Integral as the Limit of a Sum
- Evaluation of Simple Integrals of the Following Types and Problems
Sets
- Sets
Applications of the Integrals
Differential Equations
- Differential Equations
- Order and Degree of a Differential Equation
- General and Particular Solutions of a Differential Equation
- Linear Differential Equations
- Homogeneous Differential Equations
- Solutions of Linear Differential Equation
- Differential Equations with Variables Separable Method
- Formation of a Differential Equation Whose General Solution is Given
- Procedure to Form a Differential Equation that Will Represent a Given Family of Curves
Vectors
- Introduction of Vector
- Basic Concepts of Vector Algebra
- Direction Cosines
- Vectors and Their Types
- Addition of Vectors
- Properties of Vector Addition
- Multiplication of a Vector by a Scalar
- Components of Vector
- Vector Joining Two Points
- Section Formula
- Vector (Or Cross) Product of Two Vectors
- Scalar (Or Dot) Product of Two Vectors
- Projection of a Vector on a Line
- Geometrical Interpretation of Scalar
- Scalar Triple Product of Vectors
- Position Vector of a Point Dividing a Line Segment in a Given Ratio
- Magnitude and Direction of a Vector
- Vectors Examples and Solutions
- Introduction of Product of Two Vectors
Three - Dimensional Geometry
- Introduction of Three Dimensional Geometry
- Direction Cosines and Direction Ratios of a Line
- Relation Between Direction Ratio and Direction Cosines
- Equation of a Line in Space
- Angle Between Two Lines
- Shortest Distance Between Two Lines
- Three - Dimensional Geometry Examples and Solutions
- Equation of a Plane Passing Through Three Non Collinear Points
- Intercept Form of the Equation of a Plane
- Coplanarity of Two Lines
- Distance of a Point from a Plane
- Angle Between Line and a Plane
- Angle Between Two Planes
- Vector and Cartesian Equation of a Plane
- Equation of a Plane in Normal Form
- Equation of a Plane Perpendicular to a Given Vector and Passing Through a Given Point
- Distance of a Point from a Plane
- Plane Passing Through the Intersection of Two Given Planes
Linear Programming
Probability
- Introduction of Probability
- Conditional Probability
- Properties of Conditional Probability
- Multiplication Theorem on Probability
- Independent Events
- Bayes’ Theorem
- Variance of a Random Variable
- Probability Examples and Solutions
- Random Variables and Its Probability Distributions
- Mean of a Random Variable
- Bernoulli Trials and Binomial Distribution
Definition
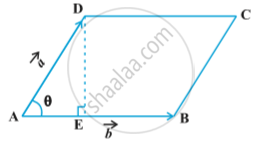
The vector product of two nonzero vectors , is denoted by and defined as
where ,θ is the angle between , 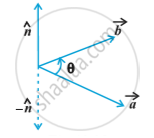
i.e., the right handed system rotated from
If either
Notes
Observations:
1)
2) Let
In particular ,
3) If , θ =
4) In view of the Observations 2 and 3, for mutually perpendicular unit vectors 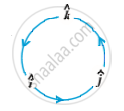
5) In terms of vector product, the angle between two vectors
6) It is always true that the vector product is not commutative, as
Indeed 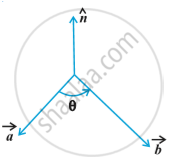
While ,
Fig.
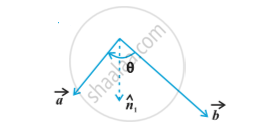
Thus, if we assume
Hence
=
= -
7) In view of the Observations 4 and 6, we have
8) If
By definition of the area of a triangle, we have from fig.
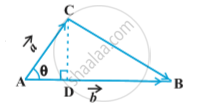
Area of triangle ABC =
But AB =
Thus, Area of triangle ABC =
9) If