Topics
Relations and Functions
Relations and Functions
Inverse Trigonometric Functions
Algebra
Calculus
Matrices
- Introduction of Matrices
- Order of a Matrix
- Types of Matrices
- Equality of Matrices
- Introduction of Operations on Matrices
- Addition of Matrices
- Multiplication of a Matrix by a Scalar
- Properties of Matrix Addition
- Properties of Scalar Multiplication of a Matrix
- Multiplication of Matrices
- Properties of Multiplication of Matrices
- Transpose of a Matrix
- Properties of Transpose of the Matrices
- Symmetric and Skew Symmetric Matrices
- Invertible Matrices
- Inverse of a Matrix by Elementary Transformation
- Multiplication of Two Matrices
- Negative of Matrix
- Subtraction of Matrices
- Proof of the Uniqueness of Inverse
- Elementary Transformations
- Matrices Notation
Determinants
- Introduction of Determinant
- Determinants of Matrix of Order One and Two
- Determinant of a Matrix of Order 3 × 3
- Area of a Triangle
- Minors and Co-factors
- Inverse of a Square Matrix by the Adjoint Method
- Applications of Determinants and Matrices
- Elementary Transformations
- Properties of Determinants
- Determinant of a Square Matrix
- Rule A=KB
Vectors and Three-dimensional Geometry
Linear Programming
Continuity and Differentiability
- Concept of Continuity
- Algebra of Continuous Functions
- Concept of Differentiability
- Derivatives of Composite Functions - Chain Rule
- Derivatives of Implicit Functions
- Derivatives of Inverse Trigonometric Functions
- Exponential and Logarithmic Functions
- Logarithmic Differentiation
- Derivatives of Functions in Parametric Forms
- Second Order Derivative
- Derivative - Exponential and Log
- Proof Derivative X^n Sin Cos Tan
- Infinite Series
- Higher Order Derivative
- Continuous Function of Point
- Mean Value Theorem
Applications of Derivatives
- Introduction to Applications of Derivatives
- Rate of Change of Bodies or Quantities
- Increasing and Decreasing Functions
- Maxima and Minima
- Maximum and Minimum Values of a Function in a Closed Interval
- Simple Problems on Applications of Derivatives
- Graph of Maxima and Minima
- Approximations
- Tangents and Normals
Probability
Integrals
- Introduction of Integrals
- Integration as an Inverse Process of Differentiation
- Some Properties of Indefinite Integral
- Methods of Integration: Integration by Substitution
- Integration Using Trigonometric Identities
- Integrals of Some Particular Functions
- Methods of Integration: Integration Using Partial Fractions
- Methods of Integration: Integration by Parts
- Fundamental Theorem of Calculus
- Evaluation of Definite Integrals by Substitution
- Properties of Definite Integrals
- Definite Integrals
- Indefinite Integral Problems
- Comparison Between Differentiation and Integration
- Geometrical Interpretation of Indefinite Integrals
- Indefinite Integral by Inspection
- Definite Integral as the Limit of a Sum
- Evaluation of Simple Integrals of the Following Types and Problems
Sets
- Sets
Applications of the Integrals
Differential Equations
- Differential Equations
- Order and Degree of a Differential Equation
- General and Particular Solutions of a Differential Equation
- Linear Differential Equations
- Homogeneous Differential Equations
- Solutions of Linear Differential Equation
- Differential Equations with Variables Separable Method
- Formation of a Differential Equation Whose General Solution is Given
- Procedure to Form a Differential Equation that Will Represent a Given Family of Curves
Vectors
- Introduction of Vector
- Basic Concepts of Vector Algebra
- Direction Cosines
- Vectors and Their Types
- Addition of Vectors
- Properties of Vector Addition
- Multiplication of a Vector by a Scalar
- Components of Vector
- Vector Joining Two Points
- Section Formula
- Vector (Or Cross) Product of Two Vectors
- Scalar (Or Dot) Product of Two Vectors
- Projection of a Vector on a Line
- Geometrical Interpretation of Scalar
- Scalar Triple Product of Vectors
- Position Vector of a Point Dividing a Line Segment in a Given Ratio
- Magnitude and Direction of a Vector
- Vectors Examples and Solutions
- Introduction of Product of Two Vectors
Three - Dimensional Geometry
- Introduction of Three Dimensional Geometry
- Direction Cosines and Direction Ratios of a Line
- Relation Between Direction Ratio and Direction Cosines
- Equation of a Line in Space
- Angle Between Two Lines
- Shortest Distance Between Two Lines
- Three - Dimensional Geometry Examples and Solutions
- Equation of a Plane Passing Through Three Non Collinear Points
- Intercept Form of the Equation of a Plane
- Coplanarity of Two Lines
- Distance of a Point from a Plane
- Angle Between Line and a Plane
- Angle Between Two Planes
- Vector and Cartesian Equation of a Plane
- Equation of a Plane in Normal Form
- Equation of a Plane Perpendicular to a Given Vector and Passing Through a Given Point
- Distance of a Point from a Plane
- Plane Passing Through the Intersection of Two Given Planes
Linear Programming
Probability
- Introduction of Probability
- Conditional Probability
- Properties of Conditional Probability
- Multiplication Theorem on Probability
- Independent Events
- Bayes’ Theorem
- Variance of a Random Variable
- Probability Examples and Solutions
- Random Variables and Its Probability Distributions
- Mean of a Random Variable
- Bernoulli Trials and Binomial Distribution
Definition
The vector product of two nonzero vectors , is denoted by and defined as `vec a xx vec b = |vec a| |vec b| sin theta hat n`,
where ,θ is the angle between , `vec a` and `vec b` = 0 ≤ θ ≤ π and `hat n` is a unit vector perpendicular to both `vec a` and `vec b`, such that `vec a`, `vec b` and `hat n` form a right handed system in following fig . 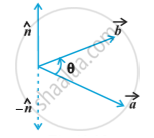
i.e., the right handed system rotated from `vec a` to `vec b` moves in the direction `hat n`.
If either `vec a = vec 0` or `vec b = vec 0` , then θ is not defined and in this case, we define `vec a xx vec b = vec 0`.
Notes
Observations:
1) `vec a xx vec b` is a vector.
2) Let `vec a` and `vec b` be two nonzero vectors. Then `vec a xx vec b = vec 0` if and only if `vec a` and `vec b` are parallel (or collinear) to each other, i.e.,
`vec a xx vec b = vec 0 <=> vec a||vec b`
In particular , `vec a xx vec b = vec 0` and `vec a xx (-vec a) = vec 0`, since in the first situation, θ = 0 and in the second one, θ = π, making the value of sinθ to be 0.
3) If , θ = `π/2` then `vec a xx vec b = |vec a||vec b|.`
4) In view of the Observations 2 and 3, for mutually perpendicular unit vectors `hat i , hat j` and` hatk` fig.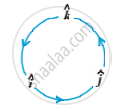
`hat i xx hat i = hat j xx hat j = hat k xx hat k = vec 0`
`hat i xx hat j = hat k , hat j xx hat k = hat i , hat k xx hat i = hat j`
5) In terms of vector product, the angle between two vectors `vec a` and `vec b` may be given as
`sin theta = (|vec a xx vec b|)/(|vec a||vec b|)`
6) It is always true that the vector product is not commutative, as `vec a xx vec b = - vec b xx vec a.`
Indeed `vec a xx vec b = |vec a||vec b| sin theta hat n_1`, where `vec b, vec a "and" hat n_1` form a right handed system, i.e., θ is traversed from `vec b "to" vec a` in following fig. 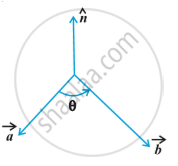
While , `vec b xx vec a = |vec a||vec b| sin theta hat n_1` , where `vec b, vec a "and" hat n_1` form a right handed system i.e. θ is traversed from `vec b " to" vec a`,
Fig.
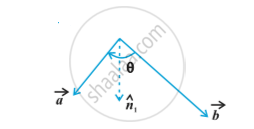
Thus, if we assume `vec a` and `vec b` to lie in the plane of the paper, then `hat n` and `hat n_1` both will be perpendicular to the plane of the paper. But, `hat n` being directed above the paper while `hat n_1` directed below the paper i.e. `hat n_1 = -hat n.`
Hence `vec a xx vec b = |vec a||vec b| sin theta hat n`
=` - |vec a||vec b| = sin theta hatn_1`
= -`vec b xx vec a =`
7) In view of the Observations 4 and 6, we have
`hat j xx hat i = - hat k , hat k xx hat j = - hat i` and `hat i xx hat k = -hat j.`
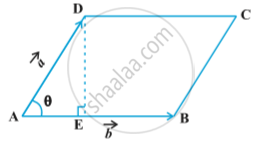
8) If `vec a` and `vec b` represent the adjacent sides of a triangle then its area is given as `1/2 |vec a xx vec b|`.
By definition of the area of a triangle, we have from fig.
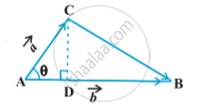
Area of triangle ABC = `1/2` AB .CD
But AB = `|vec b|` (as given ), and CD = `|vec a| sin θ. `
Thus, Area of triangle ABC = `1/2 |vec b||vec a| sin theta = 1/2 | vec a xx vec b|`.
9) If `vec a "and" vec b` represent the adjacent sides of a parallelogram, then its area is given by |vec a xx vec b|.From the following Fig. we have