Product of Two Vectors - Scalar (Or Dot) Product of Two Vectors

The scalar product of two nonzero vectors `vec a` and `vec b`, denoted by `vec a .vec b` , is defined as `vec a . vec b = |vec a| |vec b| cos theta,`
where ,  θ is the angle between Fig.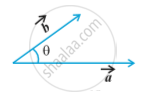

If either `vec a = 0` or `vec b = 0` then θ is not defined, and in this case , we define `vec a . vec b = 0`

Observations:
1) `vec a .vec b` is a real number.

2) Let `vec a` and `vec b` be two nonzero vectors, then `vec a . vec b = 0` if and only if `vec a` and `vec b` are perpendicular to each other . i.e.
`vec a . vec b = 0  <=> vec a ⊥ vec b`

3)  If θ = 0, then `vec a .vec b = |vec a| |vec b|`
In particular , `vec a .vec a = |vec a|^2 , as θ in this case is 0.`

4) If θ = π, then `vec a . vec b = - |vec a||vec b|`
In particular, `vec a . vec b = - |vec a||vec b|`, as θ in this case is π. 

5)  In view of the Observations 2 and 3, for mutually perpendicular unit vectors 
`hat i , hat j   "and"   hat k` we have  
`hat i . hat i = hat j . hat j = hat k. hat k = 1,`
`hat i . hat j = hat j . hat k = hat k. hat i = 0`

6) The angle between two nonzero vectors `vec a` and `vec b` is given by
`cos theta = (vec a .vec b)/(|vec a||vec b|),` or `theta = cos ^(-1)  ((vec a . vec b)/(|vec a||vec b|))`

7) The scalar product is commutative. i.e.
`vec a . vec b` = `vec b .  vec a`

Two important properties of scalar product :

Property:  (Distributivity of scalar product over addition) 
Let `vec a,  vec b` and `vec c` be any three vectors , then `vec a (vec b + vec c) = vec a . vec b + vec a. vec c`

Property:  Let `vec a` and `vec b` be any two vectors, and l be any scalar. Then
`(lambda vec a). vec b = (lambda vec a).vec b = lambda (vec a . vec b) = vec a . (lambda vec b)`
If two vectors `vec a`  and  `vec b` are given in component form as

`a_1 hat i + a_2hat j + a_3 hat k`  and  `b_1 hat i + b_2hat j + b_3 hat k .`,  then their scalar product is given as
`vec a . vec b` = `(a_1hat i + a_2 hat j + a_3 hat k) . (b_1 hat i + b_2 hat j + b_3 hat k)`
= `a_1hat i . (b_1 hat i + b_2 hat j + b_3 hat k) + a_2 hat j . (b_1 hat i + b_2 hat j + b_3 hat k) + a_3 hat k . (b_1 hat i + b_2 hat j + b_3 hat k)`
= `a_1 b_1 (hat i . hat i) + a_1b_2 (hat i . hat j) +a_1b_3 (hat i . hat k)+a_2b_1 (hat j . hat i) + a_2 b_2 (hat j . hat j) + a_2b_3 (hat j . hat k) + a_3b_1 (hat k . hat i) + a_3b_2 (hat k . hat j) + a_3b_3 (hat k . hat k)`   (Using the above Properties 1 and 2)
= `a_1b_1 + a_2b_2 + a_3b_3 `                            (Using Observation 5)

Thus `vec a . vec b = a_1b_1 + a_2b_2 + a_3b_3`