Advertisements
Advertisements
प्रश्न
Find the locus of a complex number, z = x + iy, satisfying the relation `|[ z -3i}/{z +3i]| ≤ sqrt2 `. Illustrate the locus of z in the Argand plane.
उत्तर
`|[ z -3i]/[z +3i]| ≤ sqrt2 `
⇒ `|[x + iy - 3i]/[x +iy +3i]| ≤ sqrt2 `
⇒ `|x + i (y - 3)| ≤ sqrt2 |x + i (y + 3)|`
⇒ `sqrt(x^2 + (y - 3)^2) ≤ sqrt2 sqrt(x^2 + (y + 3)^2)`
⇒ x2 + (y - 3)2 ≤ 2 (x2 + (y + 3)2)
⇒ x2 + y2 + 9 - 6y ≤ 2x2 + 2(y2 + 9 + 6y)
⇒ 2x2 + 2y2 + 18 + 12y - x2 - y2 - 9 + 6y ≥ 0
⇒ x2 + y2 + 9 + 18y ≥ 0
⇒ x2 + y2 + 18y + 9 + 81 ≥ 81
⇒ x2 + (y + 9)2 ≥ 72
⇒ (x - 0)2 + (y - (-9))2 ≥ ( 6√2)2
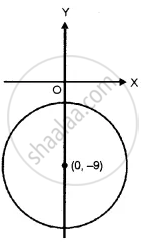
This represents a circle with centre (0, 9) and radius 6√2 units.
APPEARS IN
संबंधित प्रश्न
Write the sum of intercepts cut off by the plane `vecr.(2hati+hatj-k)-5=0` on the three axes
Find the intercepts cut off by the plane 2x + y – z = 5.
Reduce the equations of the following planes to intercept form and find the intercepts on the coordinate axes.
4x + 3y − 6z − 12 = 0
Reduce the equations of the following planes to intercept form and find the intercepts on the coordinate axes.
2x − y + z = 5
Find the equation of the plane through the point \[2 \hat{i} + \hat{j} - \hat{k} \] and passing through the line of intersection of the planes \[\vec{r} \cdot \left( \hat{i} + 3 \hat{j} - \hat{k} \right) = 0 \text{ and } \vec{r} \cdot \left( \hat{j} + 2 \hat{k} \right) = 0 .\]
Find the equation of the plane passing through the line of intersection of the planes 2x − y = 0 and 3z − y = 0 and perpendicular to the plane 4x + 5y − 3z = 8
Find the equation of the plane which contains the line of intersection of the planes x + 2y + 3z − 4 = 0 and 2x + y − z + 5 = 0 and which is perpendicular to the plane 5x + 3y − 6z+ 8 = 0.
Find the equation of the plane through the line of intersection of the planes x + 2y + 3z + 4 = 0 and x − y + z + 3 = 0 and passing through the origin.
Find the vector equation (in scalar product form) of the plane containing the line of intersection of the planes x − 3y + 2z − 5 = 0 and 2x − y + 3z − 1 = 0 and passing through (1, −2, 3).
Find the equation of the plane that is perpendicular to the plane 5x + 3y + 6z + 8 = 0 and which contains the line of intersection of the planes x + 2y + 3z − 4 = 0, 2x + y − z + 5 = 0.
Find the equation of the plane through the line of intersection of the planes \[\vec{r} \cdot \left( \hat{i} + 3 \hat{j} \right) + 6 = 0 \text{ and } \vec{r} \cdot \left( 3 \hat{i} - \hat{j} - 4 \hat{k} \right) = 0,\] which is at a unit distance from the origin.
Find the equation of the plane passing through the intersection of the planes \[\vec{r} \cdot \left( 2 \hat{i} + \hat{j} + 3 \hat{k} \right) = 7, \vec{r} \cdot \left( 2 \hat{i} + 5 \hat{j} + 3 \hat{k} \right) = 9\] and the point (2, 1, 3).
A plane makes intercepts −6, 3, 4 respectively on the coordinate axes. Find the length of the perpendicular from the origin on it.
Find the equation of the plane through the intersection of the planes 3x − y + 2z = 4 and x + y + z = 2 and the point (2, 2, 1).
Find the vector equation of the plane through the line of intersection of the planes x + y+ z = 1 and 2x + 3y + 4z = 5 which is perpendicular to the plane x − y + z = 0.
Find the vector equation of the plane passing through the intersection of the planes
\[\vec{r} \cdot \left( \hat{ i } + \hat{ j }+ \hat{ k }\right) = \text{ 6 and }\vec{r} \cdot \left( \text{ 2 } \hat{ i} +\text{ 3 } \hat{ j } + \text{ 4 } \hat{ k } \right) = - 5\] and the point (1, 1, 1).
Find the equation of the plane through the line of intersection of the planes \[x + y + z =\]1 and 2x \[+\] 3 \[+\] y \[+\] 4\[z =\] 5 and twice of its \[y\] -intercept is equal to three times its \[z\]-intercept
A plane passes through the points (2, 0, 0) (0, 3, 0) and (0, 0, 4). The equation of plane is ______.
The intercepts made by the plane 2x – 3y + 5z + 4 = 0 on the coordinate axes are `-2, 4/3, (-4)/5`.
The equation of the plane which is parallel to 2x − 3y + z = 0 and which passes through (1, −1, 2) is:
