Advertisements
Advertisements
प्रश्न
Find the magnetic field due to a long straight conductor using Ampere’s circuital law.
उत्तर
Consider a straight conductor of infinite length carrying current I and the direction of magnetic field lines. Since the wire is geometrically cylindrical in shape C and symmetrical about its axis, we construct an Amperian loop in the form of a circular shape at a distance r from the centre of the conductor. From the Ampere’s law, we get
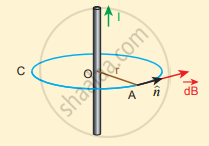
Ampèrian loop for current carrying straight wire
`oint_"C" vec"B"*"d"vec"l" = mu_0 "I"`
Where dl is the line element along the amperian loop (tangent to the circular loop). Hence, the angle between the magnetic field vector and line element is zero. Therefore,
`oint_"C" "B"*"dl" = mu_0 "I"`
where I is the current enclosed by the Amperian loop. Due to the symmetry, the magnitude of the magnetic field is uniform over the Amperian loop, we can take B out of the integration.
`"B"oint_"C" "dl" = mu_0"I"`
For a circular loop, the circumference is 2πr, which implies,
`"B"int_hat"n"^(2pi"r") "dl" = mu_0 "I"`
`vec"B"*2pi"r" = mmu_0"I"`
`=> vec"B" = (mu_0"I")/(2pi"r")`
In vector form, the magnetic field is
`vec"B" = (mu_0"I")/(2pi"r")hat"n"`
Where `hat"n"` is the unit vector along the tangent to the Amperian loop. This perfectly agrees with the result obtained from Biot-Savarf s law as given in equation
`vec"B" = (mu_0"I")/(2pi"a") hat"n"`
APPEARS IN
संबंधित प्रश्न
A 3.0 cm wire carrying a current of 10 A is placed inside a solenoid perpendicular to its axis. The magnetic field inside the solenoid is given to be 0.27 T. What is the magnetic force on the wire?
A long straight wire of a circular cross-section of radius ‘a’ carries a steady current ‘I’. The current is uniformly distributed across the cross-section. Apply Ampere’s circuital law to calculate the magnetic field at a point ‘r’ in the region for (i) r < a and (ii) r > a.
In Ampere's \[\oint \vec{B} \cdot d \vec{l} = \mu_0 i,\] the current outside the curve is not included on the right hand side. Does it mean that the magnetic field B calculated by using Ampere's law, gives the contribution of only the currents crossing the area bounded by the curve?
In order to have a current in a long wire, it should be connected to a battery or some such device. Can we obtain the magnetic due to a straight, long wire by using Ampere's law without mentioning this other part of the circuit?
Consider the situation described in the previous problem. Suppose the current i enters the loop at the points A and leaves it at the point B. Find the magnetic field at the centre of the loop.
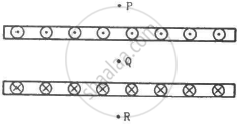
Two large metal sheets carry currents as shown in figure. The current through a strip of width dl is Kdl where K is a constant. Find the magnetic field at the points P, Q and R.
The wires which connect the battery of an automobile to its starting motor carry a current of 300 A (for a short time). What is the force per unit length between the wires if they are 70 cm long and 1.5 cm apart? Is the force attractive or repulsive?
Two identical current carrying coaxial loops, carry current I in an opposite sense. A simple amperian loop passes through both of them once. Calling the loop as C ______.
- `oint B.dl = +- 2μ_0I`
- the value of `oint B.dl` is independent of sense of C.
- there may be a point on C where B and dl are perpendicular.
- B vanishes everywhere on C.
