Advertisements
Advertisements
प्रश्न
Five forces \[\overrightarrow{AB,} \overrightarrow { AC,} \overrightarrow{ AD,}\overrightarrow{AE}\] and \[\overrightarrow{AF}\] act at the vertex of a regular hexagon ABCDEF. Prove that the resultant is 6 \[\overrightarrow{AO,}\] where O is the centre of hexagon.
उत्तर
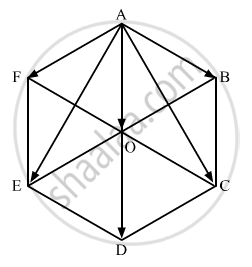
\[\overrightarrow{AB} + \overrightarrow {AC} + \overrightarrow{AD} + \overrightarrow{AE} + \overrightarrow{AF}\]
Consider ∆ADE,
\[\begin{array}{l}\overrightarrow{AD} + \overrightarrow{DE} + \overrightarrow{EA} = 0 \\ \overrightarrow{AD} + \overrightarrow{DE} = \overrightarrow{AE} \\ 2 \overrightarrow{AO} + \left( - \overrightarrow{AB} \right) =\overrightarrow{AE} \left[ \overrightarrow{AD} = 2 \overrightarrow{AO} \hspace{0.167em} \hspace{0.167em}\text{ and }ED ||\hspace{0.167em}AB \hspace{0.167em} \hspace{0.167em} \overrightarrow{DE} = - \overrightarrow{AB} \right] \\ \therefore \hspace{0.167em} \hspace{0.167em} \overrightarrow{AE} + \overrightarrow{AB} = 2 \overrightarrow{AO} . . . . . (1)\end{array}\]
Now, consider ∆ADC
\[\overrightarrow{AC} + \overrightarrow{CD} + \overrightarrow{DA} = 0\]
\[ \overrightarrow{AC} + \overrightarrow{CD} = \overrightarrow{AD} \left[ \because \overrightarrow{CD} = \overrightarrow{AF} \right]\]
\[ \overrightarrow{AC} + \overrightarrow{AF} = 2 \overrightarrow{AO} . . . . . \left( 2 \right)\]
Using (1) and (2),
\[\overrightarrow{AB} +\overrightarrow{AE} + \overrightarrow{AC} +\overrightarrow{AF}+\overrightarrow{AD} \]
\[ 2\overrightarrow{AO} + 2\overrightarrow{AO} + 2\overrightarrow{AO}\]
= \[6\overrightarrow{AO}\]
APPEARS IN
संबंधित प्रश्न
Answer the following as true or false:
\[\vec{a}\] and \[\vec{a}\] are collinear.
Answer the following as true or false:
Two collinear vectors are always equal in magnitude.
Answer the following as true or false:
Zero vector is unique.
Answer the following as true or false:
Two vectors having same magnitude are collinear.
If \[\vec{a}\] is a vector and m is a scalar such that m \[\vec{a}\] = \[\vec{0}\], then what are the alternatives for m and \[\vec{a}\] ?
If O is a point in space, ABC is a triangle and D, E, F are the mid-points of the sides BC, CA and AB respectively of the triangle, prove that \[\vec{OA} + \vec{OB} + \vec{OC} = \vec{OD} + \vec{OE} + \vec{OF}\]
If the vectors \[\vec{a} = 2 \hat{i} - 3 \hat{j}\] and \[\vec{b} = - 6 \hat{i} + m \hat{j}\] are collinear, find the value of m.
Show that the points A (1, −2, −8), B (5, 0, −2) and C (11, 3, 7) are collinear, and find the ratio in which B divides AC.
Using vectors show that the points A (−2, 3, 5), B (7, 0, −1) C (−3, −2, −5) and D (3, 4, 7) are such that AB and CD intersect at the point P (1, 2, 3).
Prove that the following vectors are coplanar:
\[\hat{i} + \hat{j} + \hat{k} , 2 \hat{i} + 3 \hat{j} - \hat{k}\text{ and }- \hat{i} - 2 \hat{j} + 2 \hat{k}\]
If \[\vec{a}\], \[\vec{a}\], \[\vec{c}\] are non-coplanar vectors, prove that the following vectors are non-coplanar: \[2 \vec{a} - \vec{b} + 3 \vec{c} , \vec{a} + \vec{b} - 2 \vec{c}\text{ and }\vec{a} + \vec{b} - 3 \vec{c}\]
If \[\vec{a}\], \[\vec{a}\], \[\vec{c}\] are non-coplanar vectors, prove that the following vectors are non-coplanar: \[\vec{a} + 2 \vec{b} + 3 \vec{c} , 2 \vec{a} + \vec{b} + 3 \vec{c}\text{ and }\vec{a} + \vec{b} + \vec{c}\]
If \[\vec{a} \cdot \text{i} = \vec{a} \cdot \left( \hat{i} + \hat{j} \right) = \vec{a} \cdot \left( \hat{i} + \hat{j} + \hat{k} \right) = 1,\] then \[\vec{a} =\]
Let \[\vec{a} \text{ and } \vec{b}\] be two unit vectors and α be the angle between them. Then, \[\vec{a} + \vec{b}\] is a unit vector if
The vector (cos α cos β) \[\hat{i}\] + (cos α sin β) \[\hat{j}\] + (sin α) \[\hat{k}\] is a
If the position vectors of P and Q are \[\hat{i} + 3 \hat{j} - 7 \hat{k} \text{ and } 5 \text{i} - 2 \hat{j} + 4 \hat{k}\] then the cosine of the angle between \[\vec{PQ}\] and y-axis is
If \[\vec{a} \text{ and } \vec{b}\] are unit vectors, then which of the following values of \[\vec{a} . \vec{b}\] is not possible?
The vector component of \[\vec{b}\] perpendicular to \[\vec{a}\] is
What is the length of the longer diagonal of the parallelogram constructed on \[5 \vec{a} + 2 \vec{b} \text{ and } \vec{a} - 3 \vec{b}\] if it is given that \[\left| \vec{a} \right| = 2\sqrt{2}, \left| \vec{b} \right| = 3\] and the angle between \[\vec{a} \text{ and } \vec{b}\] is π/4?
If θ is the angle between two vectors `veca` and `vecb` then, `veca * vecb` ≥ 0, only when
The values of x for which the angle between \[\vec{a} = 2 x^2 \hat{i} + 4x \hat{j} + \hat{k} , \vec{b} = 7 \hat{i} - 2 \hat{j} + x \hat{k}\] is obtuse and the angle between \[\vec{b}\] and the z-axis is acute and less than \[\frac{\pi}{6}\] are
If \[\vec{a} , \vec{b} , \vec{c}\] are any three mutually perpendicular vectors of equal magnitude a, then \[\left| \vec{a} + \vec{b} + \vec{c} \right|\] is equal to
The projection of the vector \[\hat{i} + \hat{j} + \hat{k}\] along the vector of \[\hat{j}\] is
If \[\left| \vec{a} \right| = \left| \vec{b} \right|, \text{ then } \left( \vec{a} + \vec{b} \right) \cdot \left( \vec{a} - \vec{b} \right) =\]
If \[\vec{a} \text{ and } \vec{b}\] are unit vectors inclined at an angle θ, then the value of \[\left| \vec{a} - \vec{b} \right|\]
If \[\vec{a} \text{ and } \vec{b}\] are unit vectors, then the greatest value of \[\sqrt{3}\left| \vec{a} + \vec{b} \right| + \left| \vec{a} - \vec{b} \right|\]
The orthogonal projection of \[\vec{a} \text{ on } \vec{b}\] is
In Figure ABCD is a regular hexagon, which vectors are:
(i) Collinear
(ii) Equal
(iii) Coinitial
(iv) Collinear but not equal.
