Advertisements
Advertisements
प्रश्न
Identify which of if the following relations are reflexive, symmetric, and transitive.
| Relation | Reflexive | Symmetric | Transitive |
| R = {(a, b) : a, b ∈ Z, a – b is an integer} | |||
| R = {(a, b) : a, b ∈ N, a + b is even} | √ | √ | x |
| R = {(a, b) : a, b ∈ N, a divides b} | |||
| R = {(a, b) : a, b ∈ N, a2 – 4ab + 3b2 = 0} | |||
| R = {(a, b) : a is sister of b and a, b ∈ G = Set of girls} | |||
| R = {(a, b) : Line a is perpendicular to line b in a plane} | |||
| R = {(a, b) : a, b ∈ R, a < b} | |||
| R = {(a, b) : a, b ∈ R, a ≤ b3} |
उत्तर
i. R = {(a, b)/a, b ∈ Z, a - b is an integer}
Let a, b, c ∈ Z
∵ a − a = 0 ∈ Z
∴ aRa ∀ a ∈ Z
∴ R is reflective
Let aRb ∴ a − b is an integer
∴ −(a − b) = b − a is also an integer
∴ bRa
∴ aRb ⇒ bRa ∀ a, b ∈ Z
∴ R is symmetric
Let aRb, bRc
∴ a − b, b − c are integers
∴ (a − b) + (b − c) = a − c is an integer
∴ aRb, bRc ⇒ aRc ∀ a, b, c ∈ Z
∴ R is transitive.
ii. R = {(a, b) / a, b ∈ N, a + b is even}
Let a, b, c ∈ N
a + a = 2a is even
∴ aRa ∀ a ∈ N
R is reflexive
Let aRb . ·. a + b is even
∴ b + a is even
∴ bRa
∴ aRb ⇒ bRa ∀ a, b ∈ N
∴ R is symmetric
Let aRb, bRc
∴ a + b, b + c are even
Let a + b = 2m, b + c = 2n
∴ (a + b) + (b + c) = 2m + 2n
∴ a + c = 2m + 2n -− 2b = 2 (m + n − b) is even
∴ aRc
∴ aRb, bRc ⇒ aRc ∀ a, b, c ∈ N
∴ R is transitive.
iii. R = {(a, b) / a, b ∈ N, a divides b}
∵ a divides a aRa ∀ a ∈ N
∵ R is reflexive
Let a = 2, b = 4
∴ 2 divides 4 so that aRb
But 4 does not divide 2 ∴ `bcancelRa`
∴ aRb `cancel=> bRc`
∴ R is not symmetric
Let aRb, bRc
∴ a divides b, b divides c
∴ b = am, c = bn, m, n ∈ N
∴ c = bn = (am)n = a(mn)
∴ a divides c ∴ aRc
∴ aRb, bRc ⇒ aRc ∀ a, b, c ∈ N
∴ R is transitive.
iv. R = {(a, b) / a, b ∈ N, a2 − 4ab + 3b2 = 0}
aRb if a2 − 4ab + 3b2 = 0
i.e., if (a − b)(a − 3b) = 0
i.e., if a = b or a = 3b
a = a ∴ aRa ∀ a ∈ N
R is reflexive
Let a = 27, b = 9
∴ a = 3b ∴ aRb
`b cancel=a and b cancel= 3a`
`b cancelRa`
`bRb cancel=> bRa`
R is not symmetric
Let a = 27, b = 9, c = 3
a = 3b ∴ aRb
Also, b = 3c ∴ bRc
But `a cancel= c and a cancel= 3c`
`a cancelR c`
`aRb, bRc cancel=> aRc`
R is not transitive.
v. R = {(a, b) / a is a sister of b,
a, b ∈ G = Set of girls}
No girl is her own sister
`a cancelR a` for any a ∈ G
R is not reflexive
Let aRb
a is a sister of b
b is a sister of a
bRa
aRb ⇒ bRa ∀ a, b ∈ G
R is symmetric
Let aRb, bRc
a is a sister of b and b is a sister of c
aRc
aRb, bRc ⇒ aRc ∀ a, b, c ∈ G
R is transitive.
vi. R = {(a, b) / Line a is perpendicular to line b in a plane}
No line is perpendicular to itself
`a cancelR a` for any line
R is not reflexive
Let aRb
a is perpendicular to b
b is perpendicular to a
bRa
aRb ⇒ bRa ∀ a, b
R is symmetric
If a is perpendicular to b and b is perpendicular to c, then a is parallel to c
aRb, bRc `cancel=>` aRc
R is not transitive.
vii. R = {(a, b) / a, be R, a < b}
a ≮ a ∀ a ∈ R
R is not reflexive
Let a = 2, b = 4
a< b
aRb
But b ≮ a
b `cancelR` a
`aRb cancel=> bRa`
R is not symmetric
Let aRb, bRc
a < b, b < c
a < b < c i.e., a < c
aRc
aRb, bRc ⇒ aRc ∀ a, b, c ∈ R
R is transitive.
viii. R = {(a, b) / a, b ∈ R, a ≤ b3 }
Let a = −2
a3 = −8
But −2 > −8
`a cancel≤ a^3` for all a ∈ R
R is not reflexive
Let a = 1, b = 2 so that a3 = 1, b3 = 8
a < b3 ...aRb
But b > a3 `bcancelRa`
aRb ~ bRa
R is not symmetric
Let a = 8, b = 2, c = 1.5
a = b3 ...aRb
c3 = (1.5)3 = 3.375
b < c3
bRc
But a < c3
aRb, bRc `cancel=>` aRc
R is not transitive.
| Relation | Reflexive | Symmetric | Transitive |
| R = {(a, b) : a, b ∈ Z, a – b is an integer} | √ | √ | √ |
| R = {(a, b) : a, b ∈ N, a + b is even} | √ | √ | √ |
| R = {(a, b) : a, b ∈ N, a divides b} | √ | x | √ |
| R = {(a, b) : a, b ∈ N, a2 – 4ab + 3b2 = 0} | √ | x | x |
| R = {(a, b) : a is sister of b and a, b ∈ G = Set of girls} | x | √ | √ |
| R = {(a, b) : Line a is perpendicular to line b in a plane} | x | √ | x |
| R = {(a, b) : a, b ∈ R, a < b} | x | x | √ |
| R = {(a, b) : a, b ∈ R, a ≤ b3} | x | x | √ |
APPEARS IN
संबंधित प्रश्न
Define a relation R on the set N of natural numbers by R = {(x, y): y = x + 5, x is a natural number less than 4; x, y ∈ N}. Depict this relationship using roster form. Write down the domain and the range.
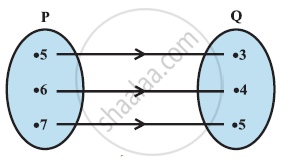
The given figure shows a relationship between the sets P and Q. Write this relation
- in set-builder form.
- in roster form.
What is its domain and range?
Let A = {x, y, z} and B = {1, 2}. Find the number of relations from A to B.
Let R be the relation on Z defined by R = {(a, b): a, b ∈ Z, a – b is an integer}. Find the domain and range of R.
Let A = (x, y, z) and B = (a, b). Find the total number of relations from A into B.
Let A = [1, 2, 3, ......., 14]. Define a relation on a set A by
R = {(x, y) : 3x − y = 0, where x, y ∈ A}.
Depict this relationship using an arrow diagram. Write down its domain, co-domain and range.
Let R be a relation on N × N defined by
(a, b) R (c, d) ⇔ a + d = b + c for all (a, b), (c, d) ∈ N × N
Show that:
(i) (a, b) R (a, b) for all (a, b) ∈ N × N
If R is a relation from set A = (11, 12, 13) to set B = (8, 10, 12) defined by y = x − 3, then write R−1.
If A = [1, 3, 5] and B = [2, 4], list of elements of R, if
R = {(x, y) : x, y ∈ A × B and x > y}
A relation R is defined from [2, 3, 4, 5] to [3, 6, 7, 10] by : x R y ⇔ x is relatively prime to y. Then, domain of R is
Write the relation in the Roster Form. State its domain and range
R1 = {(a, a2)/a is prime number less than 15}
Write the relation in the Roster Form. State its domain and range
R8 = {(a, b)/b = a + 2, a ∈ z, 0 < a < 5}
Answer the following:
If A = {1, 2, 3}, B = {4, 5, 6} check if the following are relations from A to B. Also write its domain and range
R1 = {(1, 4), (1, 5), (1, 6)}
Answer the following:
If A = {1, 2, 3}, B = {4, 5, 6} check if the following are relations from A to B. Also write its domain and range
R2 = {(1, 5), (2, 4), (3, 6)}
Answer the following:
Find R : A → A when A = {1, 2, 3, 4} such that R = {(a, b)/|a − b| ≥ 0}
Answer the following:
Show that the following is an equivalence relation
R in A = {x ∈ Z | 0 ≤ x ≤ 12} given by R = {(a, b)/|a − b| is a multiple of 4}
Let A = {1, 2, 3, 7} and B = {3, 0, –1, 7}, the following is relation from A to B?
R1 = {(2, 1), (7, 1)}
A Relation R is given by the set `{(x, y)/y = x + 3, x ∈ {0, 1, 2, 3, 4, 5}}`. Determine its domain and range
Represent the given relation by
(a) an arrow diagram
(b) a graph and
(c) a set in roster form, wherever possible
{(x, y) | x = 2y, x ∈ {2, 3, 4, 5}, y ∈ {1, 2, 3, 4}
Multiple Choice Question :
Let n(A) = m and n(B) = n then the total number of non-empty relation that can be defined from A to B is ________.
Find the domain of the function f(x) = `sqrt(1 + sqrt(1 - sqrt(1 - x^2)`
Discuss the following relation for reflexivity, symmetricity and transitivity:
Let P denote the set of all straight lines in a plane. The relation R defined by “lRm if l is perpendicular to m”
Let A = {a, b, c} and R = {(a, a), (b, b), (a, c)}. Write down the minimum number of ordered pairs to be included to R to make it transitive
On the set of natural numbers let R be the relation defined by aRb if 2a + 3b = 30. Write down the relation by listing all the pairs. Check whether it is reflexive
On the set of natural numbers let R be the relation defined by aRb if 2a + 3b = 30. Write down the relation by listing all the pairs. Check whether it is equivalence
Prove that the relation “friendship” is not an equivalence relation on the set of all people in Chennai
On the set of natural numbers let R be the relation defined by aRb if a + b ≤ 6. Write down the relation by listing all the pairs. Check whether it is reflexive
On the set of natural numbers let R be the relation defined by aRb if a + b ≤ 6. Write down the relation by listing all the pairs. Check whether it is transitive
In the set Z of integers, define mRn if m − n is divisible by 7. Prove that R is an equivalence relation
Choose the correct alternative:
The number of relations on a set containing 3 elements is
Choose the correct alternative:
Let X = {1, 2, 3, 4} and R = {(1, 1), (1, 2), (1, 3), (2, 2), (3, 3), (2, 1), (3, 1), (1, 4), (4, 1)}. Then R is
If R1 = {(x, y) | y = 2x + 7, where x ∈ R and – 5 ≤ x ≤ 5} is a relation. Then find the domain and Range of R1.
Is the given relation a function? Give reasons for your answer.
f = {(x, x) | x is a real number}
Is the given relation a function? Give reasons for your answer.
s = {(n, n2) | n is a positive integer}
Let n(A) = m, and n(B) = n. Then the total number of non-empty relations that can be defined from A to B is ______.
