Advertisements
Advertisements
प्रश्न
If sin A = `3/5` and cos B = `9/41 0 < "A" < pi/2, 0 < "B" < pi/2`, find the value of sin(A + B)
उत्तर
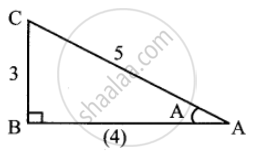
sin A = `3/5`
`0 < "A" < pi/2`
From ΔABC, AB = `sqrt(5^2 - 3^2)`
= `sqrt(25 - 9)`
= `sqrt(16)`
= 4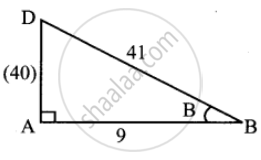
cos B = `9/41`
`0 < "B" < pi/2`
From ΔBAD, AD = `sqrt(41^2 - 9^2)`
= `sqrt((41 + 9)(41 - 9))`
= `sqrt(50 xx 32)`
= `sqrt(100 xx 16)`
= `sqrt(10^2 xx 4^2)`
= 10 × 4
= 40
Now,
From ΔABC, sin A = `3/5`, cos A = `4/5`
From ΔABD, sin B = `40/41`, cos B = `9/41`
sin(A + B) = sin A cos B + cos a sin B
= `(3/5 xx 9/4) + (4/5 xx 40/41)`
= `27/205 + 60/205`
= `187/205`
APPEARS IN
संबंधित प्रश्न
Find the value of the trigonometric functions for the following:
cos θ = `2/3`, θ lies in the I quadrant
Find sin(x – y), given that sin x = `8/17` with 0 < x < `pi/2`, and cos y = `- 24/25`, x < y < `(3pi)/2`
Prove that cos(π + θ) = − cos θ
Prove that sin 105° + cos 105° = cos 45°
Prove that sin(A + B) sin(A – B) = sin2A – sin2B
Show that tan(45° + A) = `(1 + tan"A")/(1 - tan"A")`
Show that tan(45° − A) = `(1 - tan "A")/(1 + tan "A")`
If tan x = `"n"/("n" + 1)` and tan y = `1/(2"n" + 1)`, find tan(x + y)
Prove that `32(sqrt(3)) sin pi/48 cos pi/48 cos pi/24 cos pi/12 cos pi/6` = 3
Express the following as a sum or difference
sin 35° cos 28°
Express the following as a sum or difference
2 sin 10θ cos 2θ
Express the following as a product
cos 65° + cos 15°
Show that `((cos theta -cos 3theta)(sin 8theta + sin 2theta))/((sin 5theta - sin theta) (cos 4theta - cos 6theta))` = 1
Prove that `(sin 4x + sin 2x)/(cos 4x + cos 2x)` = tan 3x
Prove that cos(30° – A) cos(30° + A) + cos(45° – A) cos(45° + A) = `cos 2"A" + 1/4`
If A + B + C = 180◦, prove that sin 2A + sin 2B + sin 2C = 4 sin A sin B sin C
If A + B + C = 180°, prove that sin2A + sin2B + sin2C = 2 + 2 cos A cos B cos C
If A + B + C = 180°, prove that sin2A + sin2B − sin2C = 2 sin A sin B cos C
Choose the correct alternative:
If cos 28° + sin 28° = k3, then cos 17° is equal to
Choose the correct alternative:
`(sin("A" - "B"))/(cos"A" cos"B") + (sin("B" - "C"))/(cos"B" cos"C") + (sin("C" - "A"))/(cos"C" cos"A")` is
