Advertisements
Advertisements
प्रश्न
If the volumes of two cones are in the ratio of 1:4 and their diameters are in the ratio of 4:5, then find the ratio of their heights.
उत्तर
Let r and R be the base radii, h and H be the heights , v and
We have,
`(2r)/(2R) = 4/5 or r/R = 4/5` ............(i)
and
`v/V = 1/4`
`rArr ((1/3pir^2h))/((1/3piR^2H))=1/4`
`rArr ((r^2h))/((R^2H)) = 1/4`
`rArr (r/R)^2xx h/H = 1/4`
`rArr (4/5)^2xxh/H = 1/4` [Using (i)]
`rArr (16/25)xx h/H=1/4`
`rArr h/H = (1xx25)/(4xx16)`
`rArr h/H = 25/64`
`therefore h: H = 25:64`
So, the ratio of their heights is 25:64.
APPEARS IN
संबंधित प्रश्न
A pen stand made of wood is in the shape of a cuboid with four conical depressions to hold pens. The dimensions of the cuboids are 15 cm by 10 cm by 3.5 cm. The radius of each of the depressions is 0.5 cm and the depth is 1.4 cm. Find the volume of wood in the entire stand (see the following figure). Use [π = `22/7`]

Find the volume of the largest right circular cone that can be cut out of a cube where edgeis 9cm?
A vessel in the shape of cuboid ontains some water. If these identical spheres are immersed in the water, the level of water is increased by 2cm. if the area of base of cuboid is 160cm2 and its height 12cm, determine radius of any of spheres?
If the radii of the circular ends of a conical bucket which is 45 cm high be 28 cm and 7 cm, find the capacity of the bucket. (Use π = 22/7).
A solid metallic cuboid of dimensions 9 m × 8 m × 2 m is melted and recast into solid cubes of edge 2 m. Find the number of cubes so formed.
The rain water from a 22 m × 20 m roof drains into a cylindrical vessel of diameter 2 m and height 3.5 m. If the rain water collected from the roof fills `4/5` th of the cylindrical vessel, then find the rainfall in centimetre.
On increasing the radii of the base and the height of a cone by 20%, its volume will increase by
Two right circular cylinders of equal volumes have their heights in the ratio 1 : 2. What is the ratio of their radii?
The figure shows a running track surrounding a grassed enclosure PQRSTU. The enclosure consists of a rectangle PQST with a semicircular region at each end, PQ = 200 m; PT = 70 meters.
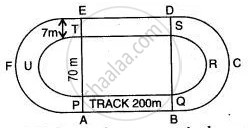
(i) Calculate the area of the grassed enclosure in m2.
(ii) Given that the track is of constant width 7 m, calculate the outer perimeter ABCDEF of the track. (Take π = `22/7`)
An ice-cream filled cone having radius 5 cm and height 10 cm is as shown in the figure. Find the volume of the ice-cream in 7 such cones.

