Advertisements
Advertisements
प्रश्न
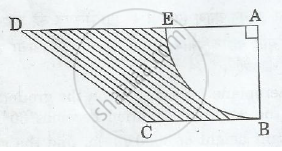
In Figure 4, from a rectangular region ABCD with AB = 20 cm, a right triangle AED with AE = 9 cm and DE = 12 cm, is cut off. On the other end, taking BC as diameter, a semicircle is added on outside the region. Find the area of the shaded region.\[[Use\pi = 3 . 14]\]

उत्तर
In right-angled ∆AED:
AD2 = AE2 + ED2
⇒ AD2 = (92 + 122) cm2
= (81 + 144) cm2
= 225 cm2
⇒ AD = 15 cm
Now, area of the rectangular region ABCD
= AB x AD
= (20 X15 ) cm2
\[ = \left( \frac{1}{2} \times 9 \times 12 \right) {cm}^2 \]
\[ = 54 {cm}^2\]
AD = BC = 15 cm
Since, BC is the diameter of the circle, therefore radius of the circle = 152 cm152 cm
Now, area of the semi-circle
\[= \frac{1}{2} \times \pi \times r^2 \]
\[ = \left( \frac{1}{2} \times 3 . 14 \times \frac{15}{2} \times \frac{15}{2} \right) {cm}^2 \]
\[ = 88 . 3125 {cm}^2\]
Area of the shaded region = Area of the rectangle + Area of the semi-circle −- Area of the triangle
= (300 + 88.3125 −- 54) cm2
= 334.3125 cm2
APPEARS IN
संबंधित प्रश्न
In Figure 2, ABCD is a trapezium of area 24.5 sq. cm. In it, AD|| BC, ∠ DAB = 900, AD = 10 cm and BC = 4 cm. If ABE is a quadrant of a circle, find the area of the shaded region. [Take π=22/7]
From a solid cylinder whose height is 2.4 cm and diameter 1.4 cm, a conical cavity of the same height and same diameter is hollowed out. Find the total surface area of the remaining solid to the nearest cm2
[use `pi = 22/7`]
A solid is composed of a cylinder with hemispherical ends. If the length of the whole solid is 108 cm and the diameter of the cylinder is 36 cm, find the cost of polishing the surface at the rate of 7 paise per cm2 .
Find the ratio of the volume of a cube to that of a sphere which will fit inside it.
The shape of the gilli used in a gilli-danda game is a combination of
A container opened at the top and made up of a metal sheet, is in the form of a frustum of a cone of height 16 cm with radii of its lower and upper ends as 8 cm and 20 cm respectively. Find the cost of milk which can completely fill the container, at the rate of ₹ 50 per litre. Also find the cost of metal sheet used to make the container, if it costs ₹ 10 per 100 cm2. (Take π = 3⋅14)
If the volumes of a cube is 1728 cm³, the length of its edge is equal to ______.
A plumbline (sahul) is the combination of (see figure) ______.
|
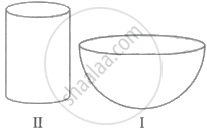
Khurja is a city in the Indian state of Uttar Pradesh famous for the pottery. Khurja pottery is traditional Indian pottery work which has attracted Indians as well as foreigners with a variety of tea sets, crockery and ceramic tile works. A huge portion of the ceramics used in the country is supplied by Khurja and is also referred as "The Ceramic Town". One of the private schools of Bulandshahr organised an Educational Tour for class 10 students to Khurja. Students were very excited about the trip. Following are the few pottery objects of Khurja.
Students found the shapes of the objects very interesting and they could easily relate them with mathematical shapes viz sphere, hemisphere, cylinder etc. |
Maths teacher who was accompanying the students asked the following questions:
- The internal radius of hemispherical bowl (filled completely with water) in I is 9 cm and the radius and height of the cylindrical jar in II are 1.5 cm and 4 cm respectively. If the hemispherical bowl is to be emptied in cylindrical jars, then how many cylindrical jars are required?
- If in the cylindrical jar full of water, a conical funnel of the same height and same diameter is immersed, then how much water will flow out of the jar?
A tent is in the shape of a cylinder surmounted by a conical top. If the height and radius of the cylindrical part are 3 m and 14 m respectively, and the total height of the tent is 13.5 m, find the area of the canvas required for making the tent, keeping a provision of 26 m2 of canvas for stitching and wastage. Also, find the cost of the canvas to be purchased at the rate of ₹ 500 per m2.