Advertisements
Advertisements
рдкреНрд░рд╢реНрди
In the following, one of the six trigonometric ratios is given. Find the values of the other trigonometric ratios.
`cot theta = 12/5`
Advertisements
рдЙрддреНрддрд░
`cot alpha = "ЁЭСОЁЭССЁЭСЧЁЭСОЁЭСРЁЭСТЁЭСЫЁЭСб ЁЭСаЁЭСЦЁЭССЁЭСТ"/"ЁЭСЬЁЭСЭЁЭСЭЁЭСЬЁЭСаЁЭСЦЁЭСбЁЭСТ ЁЭСаЁЭСЦЁЭССЁЭСТ" = 12/5`
Now consider a right-angled Δle ABC,
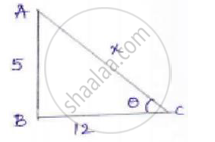
By applying Pythagoras theorem
ЁЭР┤ЁЭР╢2 = ЁЭР┤ЁЭР╡2 + ЁЭР╡ЁЭР╢2
ЁЭСе2 = 25 + 144
`x^2 = 169 = sqrt169`
ЁЭСе = 13
`tan theta = 1/cot theta = (1/12)/5 = 5/12`
`sin theta = "ЁЭСЬЁЭСЭЁЭСЭЁЭСЬЁЭСаЁЭСЦЁЭСбЁЭСТ ЁЭСаЁЭСЦЁЭССЁЭСТ"/"тДОЁЭСжЁЭСЭЁЭСЬЁЭСбЁЭСТЁЭСЫЁЭСвЁЭСаЁЭСТ" = 5/13`
`cos theta = "ЁЭСОЁЭССЁЭСЧЁЭСОЁЭСРЁЭСТЁЭСЫЁЭСб ЁЭСаЁЭСЦЁЭССЁЭСТ"/"тДОЁЭСжЁЭСЭЁЭСЬЁЭСбЁЭСТЁЭСЫЁЭСвЁЭСаЁЭСТ" = 12/13`
`cosec theta = 1/sin theta = 1/(5/13) = 13/5`
`sec theta = 1/cos theta = 1/(12/13) = 13/12`
APPEARS IN
рд╕рдВрдмрдВрдзрд┐рдд рдкреНрд░рд╢реНрди
If ∠A and ∠B are acute angles such that cos A = cos B, then show that ∠A = ∠B.
State whether the following are true or false. Justify your answer.
sec A = `12/5` for some value of angle A.
In the following, one of the six trigonometric ratios is given. Find the values of the other trigonometric ratios.
`tan theta = 8/15`
If `cos θ = 12/13`, show that `sin θ (1 - tan θ) = 35/156`.
If sin θ = `12/13`, Find `(sin^2 θ - cos^2 θ)/(2sin θ cos θ) × 1/(tan^2 θ)`.
if `cos theta = 3/5`, find the value of `(sin theta - 1/(tan theta))/(2 tan theta)`
Find the value of x in the following :
`sqrt3 sin x = cos x`
Find the value of x in the following :
cos 2x = cos 60° cos 30° + sin 60° sin 30°
If sin 2A = `1/2` tan² 45° where A is an acute angle, then the value of A is ______.
Given that sinα = `1/2` and cosβ = `1/2`, then the value of (α + β) is ______.
The value of the expression `[(sin^2 22^circ + sin^2 68^circ)/(cos^2 22^circ + cos^2 68^circ) + sin^2 63^circ + cos 63^circ sin 27^circ]` is ______.
Prove the following:
If tan A = `3/4`, then sinA cosA = `12/25`
Prove that sec θ + tan θ = `cos θ/(1 - sin θ)`.
Proof: L.H.S. = sec θ + tan θ
= `1/square + square/square`
= `square/square` ......`(тИ╡ sec θ = 1/square, tan θ = square/square)`
= `((1 + sin θ) square)/(cos θ square)` ......[Multiplying `square` with the numerator and denominator]
= `(1^2 - square)/(cos θ square)`
= `square/(cos θ square)`
= `cos θ/(1 - sin θ)` = R.H.S.
∴ L.H.S. = R.H.S.
∴ sec θ + tan θ = `cos θ/(1 - sin θ)`
Find the value of sin 45° + cos 45° + tan 45°.
`sqrt(3)` cos2A + `sqrt(3)` sin2A is equal to ______.
If b = `(3 + cot π/8 + cot (11π)/24 - cot (5π)/24)`, then the value of `|bsqrt(2)|` is ______.
If sin θ – cos θ = 0, then find the value of sin4 θ + cos4 θ.
