Advertisements
Advertisements
प्रश्न
In the following, trigonometric ratios are given. Find the values of the other trigonometric ratios.
`sec theta = 13/5`
उत्तर
`sec theta = "ℎ𝑦𝑝𝑜𝑡𝑒𝑛𝑢𝑠𝑒"/"𝑎𝑑𝑗𝑎𝑐𝑒𝑛𝑡 𝑠𝑖𝑑𝑒" = 13/5`
Now consider a right-angled Δle ABC
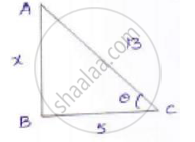
By applying Pythagoras theorem
𝐴𝐶2 = 𝐴𝐵2 + 𝐵𝐶2
169 = 𝑥2 + 25
𝑥2 = 169 − 25 = 144
𝑥 = 12
`cos theta = 1/sec theta = (1/13)/5 = 5/13`
`tan theta = "𝑜𝑝𝑝𝑜𝑠𝑖𝑡𝑒 𝑠𝑖𝑑𝑒"/"𝑎𝑑𝑗𝑎𝑐𝑒𝑛𝑡 𝑠𝑖𝑑𝑒" = 12/5`
`sin theta = "𝑜𝑝𝑝𝑜𝑠𝑖𝑡𝑒 𝑠𝑖𝑑𝑒"/"ℎ𝑦𝑝𝑜𝑡𝑒𝑛𝑢𝑠𝑒" = 12/13`
`cosect theta = 1/sin theta = 1/(12/13) = 13/12`
`sec theta = 1/cos theta = 1/(5/13) = 13/5`
`cot theta = 1/tan theta = 1/(12/5) = 5/12`
APPEARS IN
संबंधित प्रश्न
If ∠A and ∠B are acute angles such that cos A = cos B, then show that ∠A = ∠B.
In the following, one of the six trigonometric ratios is given. Find the values of the other trigonometric ratios.
tan θ = 11
In the following, trigonometric ratios are given. Find the values of the other trigonometric ratios.
`cos theta = 7/25`
Evaluate the following
`2 sin^2 30^2 - 3 cos^2 45^2 + tan^2 60^@`
Evaluate the following
`sin^2 30° cos^2 45 ° + 4 tan^2 30° + 1/2 sin^2 90° − 2 cos^2 90° + 1/24 cos^2 0°`
In ΔABC is a right triangle such that ∠C = 90° ∠A = 45°, BC = 7 units find ∠B, AB and AC
If cosec θ - cot θ = `1/3`, the value of (cosec θ + cot θ) is ______.
The value of the expression (sin 80° – cos 80°) is negative.
A ladder rests against a vertical wall at an inclination α to the horizontal. Its foot is pulled away from the wall through a distance p so that its upper end slides a distance q down the wall and then the ladder makes an angle β to the horizontal. Show that `p/q = (cos β - cos α)/(sin α - sin β)`
If `θ∈[(5π)/2, 3π]` and 2cosθ + sinθ = 1, then the value of 7cosθ + 6sinθ is ______.
