Advertisements
Advertisements
प्रश्न
Reshma wishes to mix two types of food P and Q in such a way that the vitamin contents of the mixture contains at least 8 units of vitamin A and 11 units of vitamin B. Food P costs ₹60/kg and food Q costs ₹80/kg. Food P contains 3 units/kg of vitamin A and 5 units/kg of vitamin B while food Q contains 4 units/kg of vitamin A and 2 units/kg of vitamin B. Determine the minimum cost of the mixture.
उत्तर
Let x units of food P and y units of food Q are mixed together to make the mixture.
The cost of food P is ₹60/kg and that of Q is ₹80/kg. So, x kg of food P and y kg of food Q will cost ₹(60x + 80y).
Since one kg of food P contains 3 units of vitamin A and one kg of food Q contains 4 units of vitamin A, therefore, x kg of food P and y kg of food Q will contain (3x + 4y) units of vitamin A. But, the mixture should contain atleast 8 units of vitamin A.
∴ 3x + 4y ≥ 8
Similarly, x kg of food P and y kg of food Q will contain (5x + 2y) units of vitamin B. But, the mixture should contain atleast 11 units of vitamin B.
∴ 5x + 2y ≥ 11
Thus, the given linear programming problem is
Minimise Z = 60x + 80y
subject to the constraints
3x + 4y ≥ 8
5x + 2y ≥ 11
x, y ≥ 0
The feasible region determined by the given constraints can be diagrammatically represented as,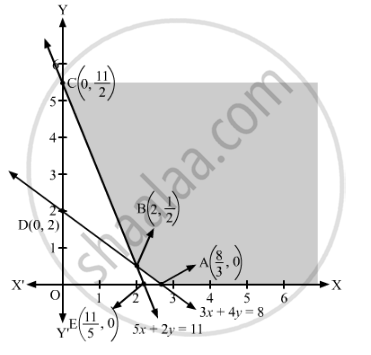
The coordinates of the corner points of the feasible region are A \[\left( \frac{8}{3}, 0 \right)\] , B \[\left( 2, \frac{1}{2} \right)\] and C \[\left( 0, \frac{11}{2} \right)\]
The value of the objective function at these points are given in the following table.
| Corner Point | Z = 60x + 80y |
|
\[\left( \frac{8}{3}, 0 \right)\]
|
\[60 \times \frac{8}{3} + 80 \times 0 = 160\] → Minimum
|
|
\[\left( 2, \frac{1}{2} \right)\]
|
\[60 \times 2 + 80 \times \frac{1}{2} = 160\] → Minimum
|
|
\[\left( 0, \frac{11}{2} \right)\]
|
\[60 \times 0 + 80 \times \frac{11}{2} = 440\]
|
The smallest value of Z is 160 which is obtained at the points \[\left( \frac{8}{3}, 0 \right)\] and \[\left( 2, \frac{1}{2} \right)\]
It can be verified that the open half-plane represented by 60x + 80y < 160 has no common points with the feasible region.
So, the minimum value of Z is 160. Hence, the minimum cost of the mixture is ₹160.
APPEARS IN
संबंधित प्रश्न
A dealer in rural area wishes to purchase a number of sewing machines. He has only Rs 5,760 to invest and has space for at most 20 items for storage. An electronic sewing machine cost him Rs 360 and a manually operated sewing machine Rs 240. He can sell an electronic sewing machine at a profit of Rs 22 and a manually operated sewing machine at a profit of Rs 18. Assuming that he can sell all the items that he can buy, how should he invest his money in order to maximize his profit? Make it as a LPP and solve it graphically.
Solve the following L.P.P graphically:
Maximize: Z = 10x + 25y
Subject to: x ≤ 3, y ≤ 3, x + y ≤ 5, x ≥ 0, y ≥ 0
Maximise Z = x + 2y subject to the constraints
`x + 2y >= 100`
`2x - y <= 0`
`2x + y <= 200`
Solve the above LPP graphically
Solve the following linear programming problem graphically :
Maximise Z = 7x + 10y subject to the constraints
4x + 6y ≤ 240
6x + 3y ≤ 240
x ≥ 10
x ≥ 0, y ≥ 0
Solve the following L.P.P graphically: Maximise Z = 20x + 10y
Subject to the following constraints x + 2y ≤ 28,
3x + y ≤ 24,
x ≥ 2,
x, y ≥ 0
Maximize Z = 10x + 6y
Subject to
\[3x + y \leq 12\]
\[2x + 5y \leq 34\]
\[ x, y \geq 0\]
Minimize Z = 2x + 4y
Subject to
\[x + y \geq 8\]
\[x + 4y \geq 12\]
\[x \geq 3, y \geq 2\]
Minimize Z = 5x + 3y
Subject to
\[2x + y \geq 10\]
\[x + 3y \geq 15\]
\[ x \leq 10\]
\[ y \leq 8\]
\[ x, y \geq 0\]
Maximize Z = 3x + 3y, if possible,
Subject to the constraints
\[x - y \leq 1\]
\[x + y \geq 3\]
\[ x, y \geq 0\]
A hospital dietician wishes to find the cheapest combination of two foods, A and B, that contains at least 0.5 milligram of thiamin and at least 600 calories. Each unit of Acontains 0.12 milligram of thiamin and 100 calories, while each unit of B contains 0.10 milligram of thiamin and 150 calories. If each food costs 10 paise per unit, how many units of each should be combined at a minimum cost?
One kind of cake requires 200 g of flour and 25 g of fat, and another kind of cake requires 100 g of flour and 50 g of fat. Find the maximum number of cakes which can be made from 5 kg of flour and 1 kg of fat assuming that there is no storage of the other ingredients used in making the cakes.
A farmer mixes two brands P and Q of cattle feed. Brand P, costing ₹250 per bag, contains 2 units of nutritional element A, 2.5 units of element B and 2 units of element C. Brand Q costing ₹200 per bag contains 1.5 units of nutritional element A, 11.25 units of element B and 3 units of element C. The minimum requirements of nutrients A, B and C are 18 units, 45 units and 24 units respectively. Determine the number of bags of each brand which should be mixed in order to produce a mixture having a minimum cost per bag? What is the minimum cost of the mixture per bag?
A firm manufactures headache pills in two sizes A and B. Size A contains 2 grains of aspirin, 5 grains of bicarbonate and 1 grain of codeine; size B contains 1 grain of aspirin, 8 grains of bicarbonate and 66 grains of codeine. It has been found by users that it requires at least 12 grains of aspirin, 7.4 grains of bicarbonate and 24 grains of codeine for providing immediate effects. Determine graphically the least number of pills a patient should have to get immediate relief. Determine also the quantity of codeine consumed by patient.
A company manufactures two types of novelty Souvenirs made of plywood. Souvenirs of type A require 5 minutes each for cutting and 10 minutes each for assembling. Souvenirs of type B require 8 minutes each for cutting and 8 minutes each for assembling. There are 3 hours 20 minutes available for cutting and 4 hours available for assembling. The profit is 50 paise each for type A and 60 paise each for type B souvenirs. How many souvenirs of each type should the company manufacture in order to maximize the profit?
A man owns a field of area 1000 sq.m. He wants to plant fruit trees in it. He has a sum of Rs 1400 to purchase young trees. He has the choice of two types of trees. Type A requires 10 sq.m of ground per tree and costs Rs 20 per tree and type B requires 20 sq.m of ground per tree and costs Rs 25 per tree. When fully grown, type A produces an average of 20 kg of fruit which can be sold at a profit of Rs 2.00 per kg and type B produces an average of 40 kg of fruit which can be sold at a profit of Rs. 1.50 per kg. How many of each type should be planted to achieve maximum profit when the trees are fully grown? What is the maximum profit?
A small firm manufacturers items A and B. The total number of items A and B that it can manufacture in a day is at the most 24. Item A takes one hour to make while item B takes only half an hour. The maximum time available per day is 16 hours. If the profit on one unit of item A be Rs 300 and one unit of item B be Rs 160, how many of each type of item be produced to maximize the profit? Solve the problem graphically.
An oil company has two depots, A and B, with capacities of 7000 litres and 4000 litres respectively. The company is to supply oil to three petrol pumps, D, E, F whose requirements are 4500, 3000 and 3500 litres respectively. The distance (in km) between the depots and petrol pumps is given in the following table:
Figure
Assuming that the transportation cost per km is Rs 1.00 per litre, how should the delivery be scheduled in order that the transportation cost is minimum?
A library has to accommodate two different types of books on a shelf. The books are 6 cm and 4 cm thick and weigh 1 kg and \[1\frac{1}{2}\] kg each respectively. The shelf is 96 cm long and atmost can support a weight of 21 kg. How should the shelf be filled with the books of two types in order to include the greatest number of books? Make it as an LPP and solve it graphically.
A cooperative society of farmers has 50 hectares of land to grow two crops X and Y. The profits from crops X and Y per hectare are estimated as ₹10,500 and ₹9,000 respectively. To control weeds, a liquid herbicide has to be used for crops X and Y at the rate of 20 litres and 10 litres per hectare, respectively. Further not more than 800 litres of herbicide should be used in order to protect fish and wildlife using a pond which collects drainage from this land. How much land should be allocated to each crop so as to maximise the total profit of the society?
A factory makes tennis rackets and cricket bats. A tennis racket takes 1.5 hours of machine time and 3 hours of craftman's time in its making while a cricket bat takes 3 hours of machine time and 1 hour of craftman's time. In a day, the factory has the availability of not more than 42 hours of machine time and 24 hours of craftman's time.
(i) What number of rackets and bats must be made if the factory is to work at full capacity?
(ii) If the profit on a racket and on a bat is Rs 20 and Rs 10 respectively, find the maximum profit of the factory when it works at full capacity.
A merchant plans to sell two types of personal computers a desktop model and a portable model that will cost Rs 25,000 and Rs 40,000 respectively. He estimates that the total monthly demand of computers will not exceed 250 units. Determine the number of units of each type of computers which the merchant should stock to get maximum profit if he does not want to invest more than Rs 70 lakhs and his profit on the desktop model is Rs 4500 and on the portable model is Rs 5000.
There are two types of fertilizers F1 and F2. F1 consists of 10% nitrogen and 6% phosphoric acid and F2 consists of 5% nitrogen and 10% phosphoric acid. After testing the soil conditions, a farmer finds the she needs atleast 14 kg of nitrogen and 14 kg of phosphoric acid for her crop. If F1 costs ₹6/kg and F2 costs ₹5/kg, determine how much of each type of fertilizer should be used so that the nutrient requirements are met at minimum cost. What is the minimum cost?
Tow godowns, A and B, have grain storage capacity of 100 quintals and 50 quintals respectively. They supply to 3 ration shops, D, E and F, whose requirements are 60, 50 and 40 quintals respectively. The cost of transportation per quintal from the godowns to the shops are given in the following table:
| Transportation cost per quintal(in Rs.) | ||
| From-> | A | B |
| To | ||
| D | 6.00 | 4.00 |
| E | 3.00 | 2.00 |
| F | 2.50 | 3.00 |
How should the supplies be transported in order that the transportation cost is minimum?
The point at which the maximum value of x + y subject to the constraints x + 2y ≤ 70, 2x + y ≤ 95, x ≥ 0, y ≥ 0 is obtained, is ______.
Maximize: z = 3x + 5y Subject to
x +4y ≤ 24 3x + y ≤ 21
x + y ≤ 9 x ≥ 0 , y ≥0
A manufacturer has employed 5 skilled men and 10 semi-skilled men and makes two models A and B of an article. The making of one item of model A requires 2 hours of work by a skilled man and 2 hours work by a semi-skilled man. One item of model B requires 1 hour by a skilled man and 3 hours by a semi-skilled man. No man is expected to work more than 8 hours per day. The manufacturer's profit on an item of model A is ₹ 15 and on an item of model B is ₹ 10. How many items of each model should be made per day in order to maximize daily profit? Formulate the above LPP and solve it graphically and find the maximum profit.
The graph of the inequality 3X − 4Y ≤ 12, X ≤ 1, X ≥ 0, Y ≥ 0 lies in fully in
The minimum value of z = 10x + 25y subject to 0 ≤ x ≤ 3, 0 ≤ y ≤ 3, x + y ≥ 5 is ______.
Area of the region bounded by y = cos x, x = 0, x = π and X-axis is ______ sq.units.
If 4x + 5y ≤ 20, x + y ≥ 3, x ≥ 0, y ≥ 0, maximum 2x + 3y is ______.
A set of values of decision variables which satisfies the linear constraints and nn-negativity conditions of an L.P.P. is called its ____________.
The corner points of the bounded feasible region of a LPP are A(0,50), B(20, 40), C(50, 100) and D(0, 200) and the objective function is Z = x + 2y. Then the maximum value is ____________.
The feasible region (shaded) for a L.P.P is shown in the figure. The maximum Z = 5x + 7y is ____________.
The objective function Z = ax + by of an LPP has maximum vaiue 42 at (4, 6) and minimum value 19 at (3, 2). Which of the following is true?
Solve the following linear programming problem graphically:
Minimize: Z = 5x + 10y
Subject to constraints:
x + 2y ≤ 120, x + y ≥ 60, x – 2y ≥ 0, x ≥ 0, y ≥ 0.
Solve the following linear programming problem graphically:
Maximize: Z = x + 2y
Subject to constraints:
x + 2y ≥ 100,
2x – y ≤ 0
2x + y ≤ 200,
x ≥ 0, y ≥ 0.
The feasible region corresponding to the linear constraints of a Linear Programming Problem is given below.
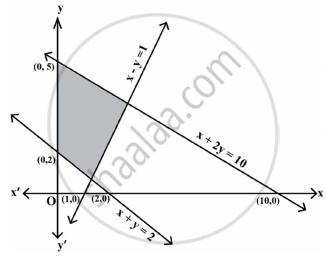
Which of the following is not a constraint to the given Linear Programming Problem?
Find feasible solution for the following system of linear inequation graphically.
3x + 4y ≥ 12, 4x + 7y ≤ 28, x ≥ 0, y ≥ 0
