Advertisements
Advertisements
प्रश्न
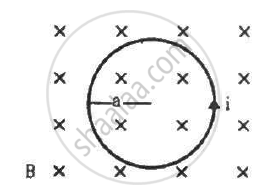
The figure shows a circular wire loop of radius a and carrying a current i, which is placed in a perpendicular magnetic field B. (a) Consider a small part dl of the wire. Find the force on this part of the wire exerted by the magnetic field. (b) Find the force of compression in the wire.
उत्तर
Given:-
Radius of the circular wire loop = a
Electric current flowing through the loop = i
Perpendicular magnetic field = B
(a) The force exerted by the magnetic field on a small element dl of the wire,
Fdl = i. (dl × B) = idlB
Using Fleming's left-hand rule, we can say that the direction of magnetic force is towards the centre for any small element of length dl of the wire (dl and B are perpendicular to each other).
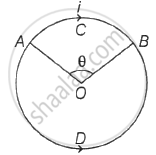
(b) Suppose some part of wire loop subtends a small angle 2θ at the centre of a circular loop
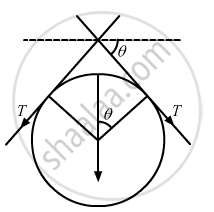
So,
2Tsinθ = i.(dl × B)
= i.2aθ B (Using length of any arc, l =rθ)
∵ θ is very small, sinθ = θ
2Tθ = i.2aθB
∴ T = iaB
APPEARS IN
संबंधित प्रश्न
Two identical circular loops, P and Q, each of radius r and carrying equal currents are
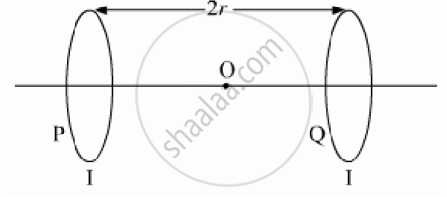
kept in the parallel planes having a common axis passing through O. The direction of current in P is clockwise and in Q is anti-clockwise as seen from O which is equidistant from the loops P and Q. Find the magnitude of the net magnetic field at O.
Is it possible for a current loop to stay without rotating in a uniform magnetic field? If yes, what should be the orientation of the loop?
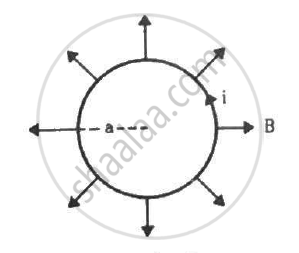
A circular loop of radius a, carrying a current i, is placed in a two-dimensional magnetic field. The centre of the loop coincides with the centre of the field (figure). The strength of the magnetic field at the periphery of the loop is B. Find the magnetic force on the wire.
A current loop of arbitrary shape lies in a uniform magnetic field B. Show that the net magnetic force acting on the loop is zero.
A 50-turn circular coil of radius 2.0 cm carrying a current of 5.0 A is rotated in a magnetic field of strength 0.20 T. (a) What is the maximum torque that acts on the coil? (b) In a particular position of the coil, the torque acting on it is half of this maximum. What is the angle between the magnetic field and the plane of the coil?
A circular loop of one turn carries a current of 5.00 A. If the magnetic field B at the centre is 0.200 mT, find the radius of the loop.
A current-carrying circular coil of 100 turns and radius 5.0 cm produces a magnetic field of 6.0 × 10−5 T at its centre. Find the value of the current.
Derive the expression for the torque acting on a current-carrying loop placed in a magnetic field.
A Rectangular coil of 10 turns, each of area 0.05 m2, is suspended freely in a uniform magnetic field of induction 0.01 T. A current of 30 µA is passed through it.
(i) What is the magnetic moment of the coil?
(ii) What is the maximum torque experienced by the coil?
A rectangular coil of length 0.12 m and width 0.1 m having 100 turns of wire is suspended vertically in a uniform magnetic field of strength 0.4 Wb/m2. The coil carries a current of 2.5 A. If the plane of the coil is inclined at an angle of 30° with the direction of the field, the torque required to keep the coil in stable equilibrium will be ____________.
A triangular loop of side `l` carries a current I. It is placed in a magnetic field B such that the plane of the loop is in the direction of B. The torque on the loop is ____________.
If in a moving coil galvanometer, a current I produces a deflection `theta,` then ____________.
If the net magnetic force acting on a loop is zero then ____________.
The sensitivity of moving coil galvanometer is inversely proportional to ____________.
In suspended type of moving coil galvanometer ____________.
Equal current i flows in two segments of a circular loop in the direction shown in figure. Radius of the loop is r. The magnitude of magnetic field induction at the centre of the loop is ______.
A thin flexible wire of length L is connected to two adjacent fixed points and carries a current I in the clockwise direction, as shown in the figure. When the system is put in a uniform magnetic field of strength B going into the plane of the paper, the wire takes the shape of a circle. The tension in the wire is ______.


Write the formula for torque acting on rotating current carrying coil in terms of magnetic dipole moment, in vector form.
