Advertisements
Advertisements
प्रश्न
Test if the following equation is dimensionally correct:
\[h = \frac{2S cos\theta}{\text{ prg }},\]
where h = height, S = surface tension, ρ = density, I = moment of interia.
उत्तर
\[h = \frac{2S \cos \theta}{\text{ prg }}\]
Height, [h] = [L]
Surface Tension,
\[\left[ S \right] = \frac{\left[ F \right]}{\left[ L \right]} = \frac{\left[ {MLT}^{- 2} \right]}{\left[ L \right]} = \left[ {MT}^{- 2} \right]\]
Density,
\[\left[ \rho \right] = \frac{\left[ M \right]}{\left[ I \right]} = \left[ {ML}^{- 3} T^0 \right]\]
Radius, [r] = [L], [g]= [LT−2]
Now,
\[\frac{2\left[ S \right]\cos \theta}{\left[ \rho \right]\left[ r \right]\left[ g \right]} = \frac{\left[ {MT}^{- 2} \right]}{\left[ {ML}^{- 3} T^0 \right] \left[ L \right] \left[ {LT}^{- 2} \right]} = \left[ M^0 L^1 T^0 \right] = \left[ L \right]\]
Since the dimensions of both sides are the same, the equation is dimensionally correct.
APPEARS IN
संबंधित प्रश्न
Some of the most profound statements on the nature of science have come from Albert Einstein, one of the greatest scientists of all time. What do you think did Einstein mean when he said : “The most incomprehensible thing about the world is that it is comprehensible”?
“Every great physical theory starts as a heresy and ends as a dogma”. Give some examples from the history of science of the validity of this incisive remark
Suppose a quantity x can be dimensionally represented in terms of M, L and T, that is, `[ x ] = M^a L^b T^c`. The quantity mass
A dimensionless quantity
Find the dimensions of linear momentum .
Find the dimensions of electric field E.
The relevant equations are \[F = qE, F = qvB, \text{ and }B = \frac{\mu_0 I}{2 \pi a};\]
where F is force, q is charge, v is speed, I is current, and a is distance.
Test if the following equation is dimensionally correct:
\[v = \sqrt{\frac{P}{\rho}},\]
where v = velocity, ρ = density, P = pressure
Test if the following equation is dimensionally correct:
\[V = \frac{\pi P r^4 t}{8 \eta l}\]
where v = frequency, P = pressure, η = coefficient of viscosity.
Test if the following equation is dimensionally correct:
\[v = \frac{1}{2 \pi}\sqrt{\frac{mgl}{I}};\]
where h = height, S = surface tension, \[\rho\] = density, P = pressure, V = volume, \[\eta =\] coefficient of viscosity, v = frequency and I = moment of interia.
Is a vector necessarily changed if it is rotated through an angle?
Is it possible to add two vectors of unequal magnitudes and get zero? Is it possible to add three vectors of equal magnitudes and get zero?
Let ε1 and ε2 be the angles made by \[\vec{A}\] and -\[\vec{A}\] with the positive X-axis. Show that tan ε1 = tan ε2. Thus, giving tan ε does not uniquely determine the direction of \[\vec{A}\].
Let \[\vec{A} = 5 \vec{i} - 4 \vec{j} \text { and } \vec{B} = - 7 \cdot 5 \vec{i} + 6 \vec{j}\]. Do we have \[\vec{B} = k \vec{A}\] ? Can we say \[\frac{\vec{B}}{\vec{A}}\] = k ?
The radius of a circle is stated as 2.12 cm. Its area should be written as
Let \[\vec{a} = 4 \vec{i} + 3 \vec{j} \text { and } \vec{b} = 3 \vec{i} + 4 \vec{j}\]. Find the magnitudes of (a) \[\vec{a}\] , (b) \[\vec{b}\] ,(c) \[\vec{a} + \vec{b} \text { and }\] (d) \[\vec{a} - \vec{b}\].
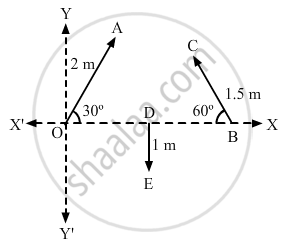
Refer to figure (2 − E1). Find (a) the magnitude, (b) x and y component and (c) the angle with the X-axis of the resultant of \[\overrightarrow{OA}, \overrightarrow{BC} \text { and } \overrightarrow{DE}\].
A mosquito net over a 7 ft × 4 ft bed is 3 ft high. The net has a hole at one corner of the bed through which a mosquito enters the net. It flies and sits at the diagonally opposite upper corner of the net. (a) Find the magnitude of the displacement of the mosquito. (b) Taking the hole as the origin, the length of the bed as the X-axis, it width as the Y axis, and vertically up as the Z-axis, write the components of the displacement vector.
Write the number of significant digits in (a) 1001, (b) 100.1, (c) 100.10, (d) 0.001001.
If π = 3.14, then the value of π2 is ______
