Advertisements
Advertisements
प्रश्न
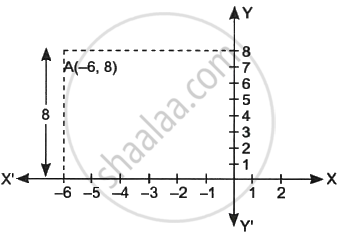
The distance of the point (–6, 8) from x-axis is ______.
विकल्प
6 units
– 6 units
8 units
10 units
उत्तर
The distance of the point (–6, 8) from x-axis is 8 units.
Explanation:
The distance of the point (x, y) from x-axis is y-coordinate
∴ The distance of the point (–6, 8) from x-axis is 8 units.
संबंधित प्रश्न
On which axis do the following points lie?
P(5, 0)
Let ABCD be a square of side 2a. Find the coordinates of the vertices of this square when The centre of the square is at the origin and coordinate axes are parallel to the sides AB and AD respectively.
Find a point on the x-axis which is equidistant from the points (7, 6) and (−3, 4).
Find the coordinates of the point where the diagonals of the parallelogram formed by joining the points (-2, -1), (1, 0), (4, 3) and(1, 2) meet
Determine the ratio in which the point P (m, 6) divides the join of A(-4, 3) and B(2, 8). Also, find the value of m.
If the point ( x,y ) is equidistant form the points ( a+b,b-a ) and (a-b ,a+b ) , prove that bx = ay
Point A lies on the line segment PQ joining P(6, -6) and Q(-4, -1) in such a way that `(PA)/( PQ)=2/5` . If that point A also lies on the line 3x + k( y + 1 ) = 0, find the value of k.
ABCD is rectangle formed by the points A(-1, -1), B(-1, 4), C(5, 4) and D(5, -1). If P,Q,R and S be the midpoints of AB, BC, CD and DA respectively, Show that PQRS is a rhombus.
Find the ratio in which the line segment joining the points A(3, 8) and B(–9, 3) is divided by the Y– axis.
Find the possible pairs of coordinates of the fourth vertex D of the parallelogram, if three of its vertices are A(5, 6), B(1, –2) and C(3, –2).
If the vertices of a triangle are (1, −3), (4, p) and (−9, 7) and its area is 15 sq. units, find the value(s) of p.
If three points (x1, y1) (x2, y2), (x3, y3) lie on the same line, prove that \[\frac{y_2 - y_3}{x_2 x_3} + \frac{y_3 - y_1}{x_3 x_1} + \frac{y_1 - y_2}{x_1 x_2} = 0\]
If \[D\left( - \frac{1}{5}, \frac{5}{2} \right), E(7, 3) \text{ and } F\left( \frac{7}{2}, \frac{7}{2} \right)\] are the mid-points of sides of \[∆ ABC\] , find the area of \[∆ ABC\] .
If P (2, p) is the mid-point of the line segment joining the points A (6, −5) and B (−2, 11). find the value of p.
If the points(x, 4) lies on a circle whose centre is at the origin and radius is 5, then x =
If A(4, 9), B(2, 3) and C(6, 5) are the vertices of ∆ABC, then the length of median through C is
The line segment joining the points A(2, 1) and B (5, - 8) is trisected at the points P and Q such that P is nearer to A. If P also lies on the line given by 2x - y + k= 0 find the value of k.
Points (1, – 1), (2, – 2), (4, – 5), (– 3, – 4) ______.
The points whose abscissa and ordinate have different signs will lie in ______.
If the points P(1, 2), Q(0, 0) and R(x, y) are collinear, then find the relation between x and y.
Given points are P(1, 2), Q(0, 0) and R(x, y).
The given points are collinear, so the area of the triangle formed by them is `square`.
∴ `1/2 |x_1(y_2 - y_3) + x_2(y_3 - y_1) + x_3(y_1 - y_2)| = square`
`1/2 |1(square) + 0(square) + x(square)| = square`
`square + square + square` = 0
`square + square` = 0
`square = square`
Hence, the relation between x and y is `square`.
