Advertisements
Advertisements
प्रश्न
The magnetic field existing in a region is given by `vecB = B_0(1 + x/1)veck` . A square loop of edge l and carrying a current i, is placed with its edges parallel to the x−y axes. Find the magnitude of the net magnetic force experienced by the loop.
उत्तर
Given:
Magnetic field, `vecB = B_0(1 + x/1)veck`
Length of the edge of a square loop = l
Electric current flowing through it = i
As per the question, the loop is placed with its edges parallel to the X−Y axes.
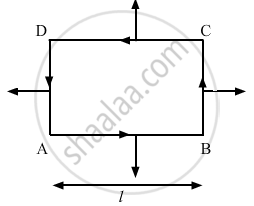
In the figure, arrow denotes the direction of force on different sides of the square.
The net magnetic force experienced by the loop,
`vecF = ivecl xx vecB`
Force on AB:
Consider a small element of length dx at a distance x from the origin on line AB.
Force on this small element,
dF = iB_0 on the full length of AB,
FAB = \[\int\limits_{x=0}^{x=0}\] iB_0 `(1 + x/l)`
= `iB_0` \[\int\limits_{x=0}^{x=0}\] `(dx + 1/l xdx)`
= `iB_0(l + 1/2)`
= `(3iBgl)/(2)`
Force on AB will be acting downwards.
Similarly, force on CD,
`F_2 = iB_0 (l + l/2)`
`=(3iBgl)/(2)`
Force on AB will be acting downwards.
Similarly, force on CD,
`F_2 = iB_0 (l + 1/2)`
= `(3iBgl)/2`
So, the net vertical force = F1 − F2 = 0
Force on AD,
`F_4 = iB_0l (1 + 1/l)`
= 2iB0l
Force on BC
`F_4 = iB_0l(1 + 1/l)`
=2iB0l
So, the net horizontal force = F4−F3 = iB0l
APPEARS IN
संबंधित प्रश्न
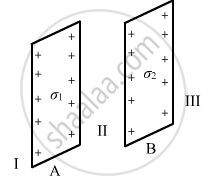
Two infinitely large plane thin parallel sheets having surface charge densities σ1 and σ2 (σ1 > σ2) are shown in the figure. Write the magnitudes and directions of the net fields in the regions marked II and III.
An electron beam projected along the positive x-axis deflects along the positive y-axis. If this deflection is caused by a magnetic field, what is the direction of the field? Can we conclude that the field is parallel to the z-axis?
A charged particle goes undeflected in a region containing an electric and a magnetic field. It is possible that
(a) `vecE" || "vecB , vecv" || " vec E `
(b) `vecE "is not parallel" vecB`
(c) `vecv " || " vecB but vecv "is not parallel"`
(d) `vecE" || " vecB but vecv "is not parallel"`
An electron is moving along the positive x-axis. You want to apply a magnetic field for a short time so that the electron may reverse its direction and move parallel to the negative x-axis. This can be done by applying the magnetic field along
(a) y-axis
(b) z-axis
(c) y-axis only
(d) z-axis only
Two parallel, long wires carry currents i1 and i2 with i1 > i2. When the currents are in the same direction, the magnetic field at a point midway between the wires is 10 µT. If the direction of i2 is reversed, the field becomes 30 µT. The ratio i1/i2 is
A current of 10 A is established in a long wire along the positive z-axis. Find the magnetic field \[\vec{B}\] at the point (1 m, 0, 0).
A transmission wire carries a current of 100 A. What would be the magnetic field B at a point on the road if the wire is 8 m above the road?
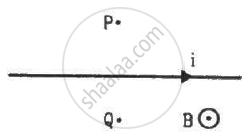
A long, straight wire carrying a current of 1.0 A is placed horizontally in a uniform magnetic field B = 1.0 × 10−5 T pointing vertically upward figure. Find the magnitude of the resultant magnetic field at the points P and Q, both situated at a distance of 2.0 cm from the wire in the same horizontal plane.
A hypothetical magnetic field existing in a region is given by `vecB = B_0 vece` where `vece`_r denotes the unit vector along the radial direction. A circular loop of radius a, carrying a current i, is placed with its plane parallel to the x−y plane and the centre at (0, 0, d). Find the magnitude of the magnetic force acting on the loop.
A rectangular coil of 100 turns has length 5 cm and width 4 cm. It is placed with its plane parallel to a uniform magnetic field and a current of 2 A is sent through the coil. Find the magnitude of the magnetic field B if the torque acting on the coil is 0.2 N m−1
A long, straight wire carries a current i. Let B1 be the magnetic field at a point P at a distance d from the wire. Consider a section of length l of this wire such that the point P lies on a perpendicular bisector of the section B2 be the magnetic field at this point due to this second only. Find the value of d/l so that B2 differs from B1 by 1%.
A milli voltmeter of 25 milli volt range is to be converted into an ammeter of 25 ampere range. The value (in ohm) of necessary shunt will be ______.
The nature of parallel and anti-parallel currents are ______.
Do magnetic forces obey Newton’s third law. Verify for two current elements dl1 = dlî located at the origin and dl2 = dlĵ located at (0, R, 0). Both carry current I.
Five long wires A, B, C, D and E, each carrying current I are arranged to form edges of a pentagonal prism as shown in figure. Each carries current out of the plane of paper.
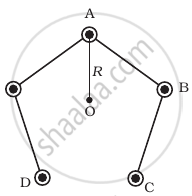
- What will be magnetic induction at a point on the axis O? AxisE is at a distance R from each wire.
- What will be the field if current in one of the wires (say A) is switched off?
- What if current in one of the wire (say) A is reversed?
Two long straight parallel conductors carrying currents I1 and I2 are separated by a distance d. If the currents are flowing in the same direction, show how the magnetic field produced by one exerts an attractive force on the other. Obtain the expression for this force and hence define 1 ampere.
Two long straight parallel current-carrying conductors are kept ‘a’ distant apart in the air. The direction of current in both the conductors is the same. Find the magnitude of force per unit length and the direction of the force between them. Hence define one ampere.
The figure below are two long, parallel wires carrying current in the same direction such that I1 < I2.
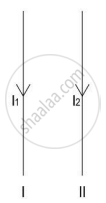
- In which direction will wire I1 move?
- If the direction of the current I2 is reversed, in which direction will the wire I1 move now?
