HSC Science (General)
HSC Arts (English Medium)
HSC Science (Electronics)
HSC Science (Computer Science)
HSC Arts (Marathi Medium)
Academic Year: 2024-2025
Date & Time: 22nd February 2025, 11:00 am
Duration: 3h
Advertisements
General Instruction:
The question paper is divided into FOUR sections.
- Section A:
Q. 1 contains Eight multiple choice type of questions, each carrying Two marks each.
Q. 2 contains Four very short answer type questions, each carrying One mark each. - Section B: This section contains Twelve short answer type questions carrying Two marks each.(Attempt any Eight)
- Section C: This section contains Twelve short answer type questions carrying Three marks each (Attempt any Eight)
- Section D: This section contains Eight long answer type questions carrying Four marks each. (Attempt any Five)
- Use of log table is allowed. Use of calculator is not allowed.
- Figures to the right indicate full marks.
- Use of graph paper is not necessary. Only rough sketch of graph is expected.
- For each multiple choice type of question; only the first attempt will be considered for evaluation.
- Start answer to each section on a new page.
If A = {1, 2, 3, 4, 5} then which of the following is not true?
∃ x ∈ A such that x + 3 = 8
∃ x ∈ A such that x + 2 < 9
∀ x ∈ A, x + 6 ≥ 9
∃ x ∈ A such that x + 6 < 10
Chapter: [0.01] Mathematical Logic [0.011000000000000001] Mathematical Logic
In ΔABC, (a + b) cos C + (b + c) cos A + (c + a) cos B is equal to ______.
a − b + c
a + b − c
a + b + c
a − b − c
Chapter:
If `|bar a|` = 5, `|bar b|` = 13 and `|bara xx barb|` = 25 then `|bar a * bar b|` is equal to ______.
30
60
40
45
Chapter:
The vector equation of the line passing through the point having position vector `4 hat i - hat j + 2hat k` and parallel to vector `-2 hat i - hat j + hat k` is given by ______.
`(4hat i - hat j - 2hat k) + lambda (-2hat i - hat j + hat k)`
`(4hat i - hat j + 2hat k) + lambda (2hat i - hat j + hat k)`
`(4hat i - hat j + 2hat k) + lambda (-2hat i - hat j - hat k)`
`(4hat i - hat j + 2hat k) + lambda (-2hat i - hat j + hat k)`
Chapter:
Let f(1) = 3, f'(1) = `-1/3`, g(1) = −4 and g'(1) = `-8/3`. The derivative of `sqrt([f(x)]^2 + [g(x)]^2` w.r.r. x at x = 1 is ______.
`-29/25`
`7/3`
`31/15`
`29/15`
Chapter:
If the mean and variance of a binomial distribution are 18 and 12 respectively, then n = ______.
36
54
18
27
Chapter: [0.027999999999999997] Binomial Distribution
The value of `intx^x (1 + logx)dx` is equal to ______.
`1/2(1 + logx)^2 + c`
`x^(2x) + c`
`x^x.logx + c`
`x^x + c`
Chapter:
The area bounded by the line y = x, X-axis and the lines x = −1 and x = 4 is equal to ______ (in square units).
`2/17`
8
`17/2`
`1/2`
Chapter:
Write the negation of the statement.
‘∃ n ∈ N such that n + 8 > 11’
Chapter:
Write unit vector in the opposite direction to `baru = 8hati + 3hatj - hatk`.
Chapter:
Write the order of the differential equation `sqrt(1 + (dy/dx)^2) = ((d^2y)/dx^2)^(3/2)`.
Chapter:
Write the condition for the function f(x) to be strictly increasing for all x ∈ R.
Chapter:
Using truth table, prove that the statement patterns p ↔ q and (p ∧ q) ∨ (~ p ∧ ~ q) are logically equivalent.
Chapter:
Find the adjoint of the matrix `[(2,-2),(4,3)]`.
Chapter:
Advertisements
Find the coordinates of the points of intersection of the lines represented by x2 − y2 − 2x + 1 = 0
Chapter: [0.013999999999999999] Pair of Straight Lines
A line makes angles of measure 45° and 60° with the positive directions of the Y and Z axes respectively. Find the angle made by the line with the positive direction of the X-axis.
Chapter:
Find the vector equation of the plane passing through the point having position vector `2hati + 3hatj + 4hatk` and perpendicular to the vector `2hati + hatj - 2hatk`.
Chapter:
Divide the number 20 into two parts such that sum of their squares is minimum.
Chapter: [0.022000000000000002] Applications of Derivatives [0.14] Applications of Derivative
Integrate the following function w.r.t. x:
x9.sec2(x10)
Chapter: [0.023] Indefinite Integration [0.15] Integration
Evaluate the following:
`int (1)/(25 - 9x^2)*dx`
Chapter: [0.023] Indefinite Integration [0.15] Integration
Evaluate:
`int_(-pi/4)^(pi/4) (1)/(1 - sinx)*dx`
Chapter: [0.024] Definite Integration
Find the area of the region bounded by the parabola y2 = 16x and its latus rectum.
Chapter: [0.025] Application of Definite Integration
Suppose that X is waiting time in minutes for a bus and its p.d.f. is given by f(x) = `1/5`, for 0 ≤ x ≤ 5 and = 0 otherwise.
Find the probability that waiting time is between 1 and 3.
Chapter: [0.027000000000000003] Probability Distributions
Suppose that X is waiting time in minutes for a bus and its p.d.f. is given by f(x) = `1/5`, for 0 ≤ x ≤ 5 and = 0 otherwise.
Find the probability that the waiting time is more than 4 minutes.
Chapter: [0.027000000000000003] Probability Distributions
Find the symbolic form of the given switching circuit. Construct its switching table and interpret your result.
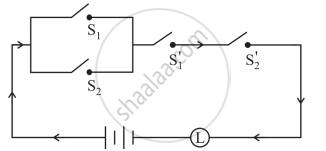
Chapter: [0.01] Mathematical Logic [0.011000000000000001] Mathematical Logic
Prove that `2 tan^(-1) (1/3) + cos^(-1) (3/5) = pi/2`.
Chapter:
In ΔABC if a = 13, b = 14, c = 15, then find the value of sec A.
Chapter:
In ΔABC if a = 13, b = 14, c = 15, then find the value of `"cosec" A/2`.
Chapter:
A line passes through the points (6, −7, −1) and (2, −3, 1). Find the direction ratios and the direction cosines of the line. Show that the line does not pass through the origin.
Chapter:
Advertisements
Find the cartesian and vector equations of the line passing through A(1, 2, 3) and having direction ratios 2, 3, 7.
Chapter:
Find the vector equation of the plane passing through points A(1, 1, 2), B(0, 2, 3) and C(4, 5, 6).
Chapter:
The displacement of a particle at time t is given by s = 2t3 − 5t2 + 4t − 3. Find the velocity and displacement at the time when the acceleration is 14 ft/sec2.
Chapter:
Find the equations of tangent and normal to the curve y = 2x3 − x2 + 2 at point `(1/2, 2)`.
Chapter:
Three coins are tossed simultaneously; X is the number of heads. Find the expected value and variance of X.
Chapter:
Solve the differential equation:
`x dy/dx = x·tan(y/x)+y`
Chapter:
Five cards are drawn successively with replacement from a well-shuffled deck of 52 cards; find the probability that all the five cards are spades.
Chapter: [0.027999999999999997] Binomial Distribution
Five cards are drawn successively with replacement from a well-shuffled deck of 52 cards; find the probability that none is a spade.
Chapter: [0.027999999999999997] Binomial Distribution
Find the inverse of A = `[("cos" theta, -"sin" theta, 0),("sin" theta, "cos" theta, 0),(0,0,1)]` by elementary row transformations.
Chapter: [0.012] Matrics
Prove that homogeneous equation of degree two in x and y, ax2 + 2hxy + by2 = 0 represents a pair of lines passing through the origin if h2 − ab ≥ 0. Hence show that equation x2 + y2 = 0 does not represent a pair of lines.
Chapter:
Let `bara` and `barb` be non-collinear vectors. If vector `barr` is coplanar with `bara` and `barb`, then show that there exist unique scalars t1 and t2 such that `barr = t_1 bara + t_2 barb`. For `barr = 2hati + 7hatj + 9hatk, bara = hati + 2hatj, barb = hatj + 3hatk`, find t1, t2.
Chapter:
Solve the Linear Programming problem graphically:
Maximize z = 3x + 5y subject to x + 4y ≤ 24, 3x + y ≤ 21, x + y ≤ 9, x ≥ 0, y ≥ 0 also find the maximum value of z.
Chapter: [0.017] Linear Programming
If x = f(t) and y = g(t) are differentiable functions of t so that y is a function of x and if `(dx)/(dt)` ≠ 0 then prove that `(dy)/(dx) = ((dy)/(dt))/((dx)/(d"))`.
Hence, find the derivative of 7x w.r.t. x7.
Chapter:
Integrate the following functions w.r.t. x : `e^(sin^-1x)*[(x + sqrt(1 - x^2))/sqrt(1 - x^2)]`
Chapter: [0.023] Indefinite Integration [0.15] Integration
Prove that: `int_a^b f(x) dx = int_a^b f(a + b - x)dx`
Hence evaluate: `int_0^3 sqrtx/(sqrtx + sqrt(3 - x)) dx`
Chapter:
If a body cools from 80°C to 50°C at room temperature of 25°C in 30 minutes, find the temperature of the body after 1 hour.
Chapter: [0.026000000000000002] Differential Equations
Other Solutions
Submit Question Paper
Help us maintain new question papers on Shaalaa.com, so we can continue to help studentsonly jpg, png and pdf files
Maharashtra State Board previous year question papers 12th Standard Board Exam Mathematics and Statistics with solutions 2024 - 2025
Previous year Question paper for Maharashtra State Board 12th Standard Board Exam Maths and Stats-2025 is solved by experts. Solved question papers gives you the chance to check yourself after your mock test.
By referring the question paper Solutions for Mathematics and Statistics, you can scale your preparation level and work on your weak areas. It will also help the candidates in developing the time-management skills. Practice makes perfect, and there is no better way to practice than to attempt previous year question paper solutions of Maharashtra State Board 12th Standard Board Exam.
How Maharashtra State Board 12th Standard Board Exam Question Paper solutions Help Students ?
• Question paper solutions for Mathematics and Statistics will helps students to prepare for exam.
• Question paper with answer will boost students confidence in exam time and also give you an idea About the important questions and topics to be prepared for the board exam.
• For finding solution of question papers no need to refer so multiple sources like textbook or guides.
