Advertisements
Advertisements
प्रश्न
A(7, 1), B(3, 5) आणि C(2, 0) शिरोबिंदू असलेल्या त्रिकोणाच्या परिवर्तुळाच्या केंद्राचे निर्देशक आणि परिवर्तुळाची त्रिज्या काढा.
उत्तर
समजा, O(h, k) हा ΔABC च्या परिवर्तुळाचा केंद्र आहे.

OA = OC .......[एकाच वर्तुळाच्या त्रिज्या]
∴ `sqrt((h - 7)^2 + (k - 1)^2) = sqrt((h - 2)^2 + (k - 0)^2)` ....[अंतराच्या सूत्रानुसार]
∴ (h - 7)2 + (k - 1)2 = (h - 2)2 + (k - 0)2 ......[दोन्ही बाजूंचे वर्ग करून]
∴ h2 - 14h + 49 + k2 - 2k + 1 = h2 - 4h + 4 + k2
∴ 10h + 2k = 46
∴ 5h + k = 23 .....(i) [दोन्ही बाजूंना 2 ने भागून]
OB = OC .....[एकाच वर्तुळाच्या त्रिज्या]
∴ `sqrt((h - 3)^2 + (k - 5)^2) = sqrt((h - 2)^2 + (k - 0)^2)` ....[अंतराच्या सूत्रानुसार]
∴ (h - 3)2 + (k - 5)2 = (h - 2)2 + (k - 0)2 .....[दोन्ही बाजूंचे वर्ग करून]
∴ h2 - 6h + 9 + k2 - 10k + 25 = h2 - 4h + 4 + k2
∴ 2h + 10k = 30
∴ h + 5k = 15 .....(ii) [दोन्ही बाजूंना 2 ने भागून]
समीकरण (i) ला 5 ने गुणून,
25h + 5k = 115 …(iii)
समीकरण (iii) मधून (ii) वजा करून,
25h + 5k = 115
h + 5k = 15
- - -
24h = 100
∴ h = `100/24 = 25/6`
h ची किंमत समीकरण (i) मध्ये ठेवून,
5h + k = 23
∴ `5(25/6) + k = 23`
∴ k = 23 - `125/6 = (138 - 125)/6`
∴ k = `13/6`
∴ O(h, k) = `(25/6, 13/6)`
अंतराच्या सूत्रानुसार,
त्रिज्या = d(O, C) = `sqrt((25/6 - 2)^2 + (13/6 - 0)^2)`
= `sqrt(((25 - 12)/6)^2 + (13/6)^2)`
= `sqrt((13/6)^2 + (13/6)^2)`
= `sqrt(2(13/6)^2)`
= `(13sqrt(2))/6` एकक
∴ त्रिकोणाच्या परिवर्तुळाच्या केंद्राचे निर्देशक `(25/6, 13/6)` आहे व त्याची त्रिज्या `(13sqrt(2))/6` एकक आहे.
APPEARS IN
संबंधित प्रश्न
खालील बिंदू एकरेषीय आहेत की नाहीत हे ठरवा.
A(1, −3), B(2, −5), C(−4, 7)
खालील बिंदू एकरेषीय आहेत की नाहीत हे ठरवा.
L(-2, 3), M(1, -3), N(5, 4)
खालील बिंदू एकरेषीय आहेत की नाहीत हे ठरवा.
R(0, 3), D(2, 1), S(3, -1)
खालील बिंदूंतील अंतर काढा.
P(-6, -3), Q(-1, 9)
खालील बिंदूंतील अंतर काढा.
R(-3a, a), S(a, -2a)
खालील बिंदूंना जोडणारे रेषाखंड त्रिकोण तयार करू शकतील का? त्रिकोण तयार झाल्यास त्याचा बाजूंवरून होणारा प्रकार सांगा.
L(6, 4) , M(-5, -3) , N(-6, 8)
खालील बिंदूंना जोडणारे रेषाखंड त्रिकोण तयार करू शकतील का? त्रिकोण तयार झाल्यास त्याचा बाजूंवरून होणारा प्रकार सांगा.
A(`sqrt2` , `sqrt2`), B(`-sqrt2` , `-sqrt2`), C(`-sqrt6`, `sqrt6`)
बिंदू Q(3, –7) आणि बिंदू R(3, 3) आहेत, तर बिंदू Q आणि R मधील अंतर किती?
उकल:
समजा, Q(x1, y1) आणि बिंदू R(x2, y2)
x1 = 3, y1 = –7 आणि x2 = 3, y2 = 3
अंतराच्या सूत्रानुसार,
d(Q, R) = `sqrtsquare`
∴ d(Q, R) = `sqrt(square - 100)`
d(Q, R) = `sqrtsquare`
∴ d(Q, R) = `sqrtsquare`
(2, 0), (–2, 0) आणि (0, 2) हे त्रिकोणाचे शिरोबिंदू आहेत हे दाखवा. तसेच त्या त्रिकोणाचा प्रकार सकारण ठरवा.
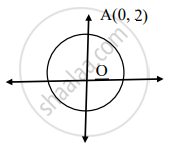
O केंद्र असलेल्या वर्तुळाची OA ही त्रिज्या आहे. जर A चे निर्देशक (0, 2) असतील तर बिंदू (1, 2) हा वर्तुळावर आहे किंवा नाही पडताळा घ्या.