Advertisements
Advertisements
प्रश्न
खालील बिंदूंना जोडणारे रेषाखंड त्रिकोण तयार करू शकतील का? त्रिकोण तयार झाल्यास त्याचा बाजूंवरून होणारा प्रकार सांगा.
L(6, 4) , M(-5, -3) , N(-6, 8)
उत्तर
अंतराच्या सूत्रानुसार,
d(L, M) = `sqrt((x_2 - x_1)^2 + (y_2 - y_1)^2)`
= `sqrt((-5 - 6)^2 + (-3 - 4)^2)`
= `sqrt((-11)^2 + (-7)^2)`
= `sqrt(121 + 49)`
∴ d(L, M) = `sqrt170` .....(i)
d(M, N) = `sqrt((x_2 - x_1)^2 + (y_2 - y_1)^2)`
= `sqrt([-6 - (-5)]^2 + [8 - (-3)]^2)`
= `sqrt((-6 + 5)^2 + (8 + 3)^2)`
= `sqrt((-1)^2 + 11^2) = sqrt(1 + 121)`
∴ d(M, N) = `sqrt122` .....(ii)
d(L, N) = `sqrt((x_2 - x_1)^2 + (y_2 - y_1)^2)`
= `sqrt((-6-6)^2 + (8 - 4)^2)`
= `sqrt((-12)^2 + (4)^2) = sqrt(144 + 16)`
∴ d(L, N) = `sqrt160` .....(iii)
(ii) आणि (iii) मिळवले असता
d(M, N) + d(L, N) = `sqrt122` + `sqrt160`
`sqrt122` + `sqrt160` > `sqrt170`
∴ d(M, N) + d(L, N) > d(L, M)
∴ बिंदू L, M आणि N हे एकरेषीय बिंदू नाहीत.
तीन नैकरेषीय बिंदूंमधून त्रिकोण तयार करता येतो.
∴ दिलेल्या बिंदूंना जोडणाऱ्या रेषाखंडांपासून त्रिकोण तयार होतो.
तसेच, MN ≠ LN ≠ LM
∴ ΔLMN हा विषमभुज त्रिकोण आहे.
∴ बिंदू L, M आणि N यांना जोडणारे रेषाखंड विषमभुज त्रिकोण तयार करतील.
APPEARS IN
संबंधित प्रश्न
खालील बिंदू एकरेषीय आहेत की नाहीत हे ठरवा.
R(0, 3), D(2, 1), S(3, -1)
X-अक्षावरील असा बिंदू शोधा की जो P(2,-5) आणि Q(-2,9) पासून समदूर असेल.
P(6,-6), Q(3,-7) आणि R(3,3) यांतून जाणाऱ्या वर्तुळाच्या केंद्राचे निर्देशक काढा.
खालील बिंदूंना जोडणारे रेषाखंड त्रिकोण तयार करू शकतील का? त्रिकोण तयार झाल्यास त्याचा बाजूंवरून होणारा प्रकार सांगा.
A(`sqrt2` , `sqrt2`), B(`-sqrt2` , `-sqrt2`), C(`-sqrt6`, `sqrt6`)
बिंदू P(–1, 1) आणि बिंदू Q(5, –7) आहेत. तर बिंदू P आणि Q मधील अंतर ______
A(0, 0), B(–5, 12) या दोन बिंदूंमधील अंतर किती?
C(–3a, a), D(a, –2a) या दोन बिंदूंमधील अंतर काढा.
सोबतच्या आकृतीत, दिलेल्या माहितीवरून त्रिकोणाच्या मध्यगेची लांबी काढण्यासाठी खालील कृती पूर्ण करा.
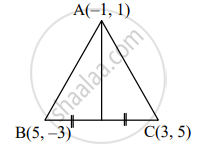
कृती: A(–1, 1), B(5, –3), C(3, 5) समजा, D(x, y)
मध्यबिंदू सूत्रानुसार,
x = `(5 + 3)/2` ∴ x = `square`
y = `(-3 + 5)/2` ∴ y = `square`
अंतराच्या सूत्रानुसार,
∴ AD = `sqrt((4 - square)^2 + (1 - 1)^2)`
∴ AD = `sqrt((square)^2 + (0)^2)`
∴ AD = `sqrtsquare`
∴ AD = `square`
(0, 9) हा बिंदू (–4, 1) व (4, 1) या बिंदूंपासून समदूर आहे हे दाखवा.
O(0, 0) आणि P(3, 4) या दोन बिंदूतील अंतर काढा.
