Advertisements
Advertisements
प्रश्न
A = (7, −2) and C = (−1, −6) are the vertices of square ABCD. Find the equations of diagonals AC and BD.
उत्तर
We know that in a square, diagonals bisect each other at right angle.
Let O be the point of intersection of the diagonals AC and BD.
Co-ordinates of O are
`((7 - 1)/2, (-2 - 6)/2) = (3, -4)`
Slope of AC = `(-6 + 2)/(-1 - 7) = (-4)/-8 = 1/2`
For line AC:
Slope = m = `1/2`, (x1, y1) = (7, –2)
Equation of the line AC is
y – y1 = m(x – x1)
`y + 2 =1/2 (x - 7)`
2y + 4 = x – 7
2y = x – 11
For line BD:
Slope = m = `(-1)/("slope of AC") = (-1)/(1/2)= -2`,
(x1, y1) = (3, −4)
Equation of the line BD is
y − y1 = m(x − x1)
y + 4 = −2(x − 3)
y + 4 = −2x + 6
2x + y = 2
APPEARS IN
संबंधित प्रश्न
Find the slope and y-intercept of the line:
ax – by = 0
The equation of a line is x – y = 4. Find its slope and y-intercept. Also, find its inclination.
The points A, B and C are (4, 0), (2, 2) and (0, 6) respectively. Find the equations of AB and BC. If AB cuts the y-axis at P and BC cuts the x-axis at Q, find the co-ordinates of P and Q.
Find the point on the X–axis which is equidistant from A(–3, 4) and B(1, –4).
Verify that points P(–2, 2), Q(2, 2) and R(2, 7) are vertices of a right angled triangle.
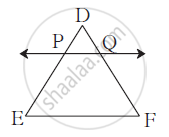
In Δ DEF, line PQ || side EF, If DP = 2.4,
PE = 7.2, DQ = 1 then find QF.
Find:
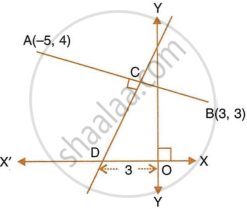
- equation of AB
- equation of CD
In the given figure, line AB meets y-axis at point A. Line through C(2, 10) and D intersects line AB at right angle at point P. Find:
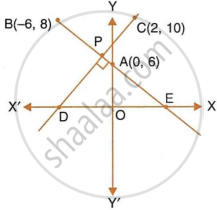
- equation of line AB.
- equation of line CD.
- co-ordinates of points E and D.
A line through point P(4, 3) meets x-axis at point A and the y-axis at point B. If BP is double of PA, find the equation of AB.
Find the equation of line through the intersection of lines 2x – y = 1 and 3x + 2y = –9 and making an angle of 30° with positive direction of x-axis.
