Advertisements
Advertisements
प्रश्न
A boy travelling in an open car moving on a levelled road with constant speed tosses a ball vertically up in the air and catches it back. Sketch the motion of the ball as observed by a boy standing on the footpath. Give explanation to support your diagram.
उत्तर
Let the vertical velocity of the tossed ball be v and the speed of the car be u which must be equal to the horizontal velocity of the ball.
The ball has both components of motion, hence it will have a parabolic trajectory when observed from a distance. This can be shown in the figure below.
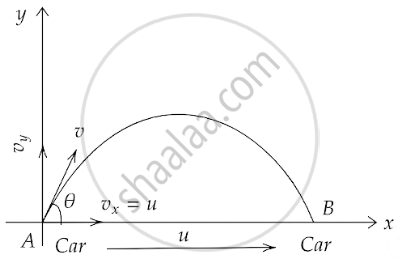
When this motion is observed by the boy sitting in the car, it will look like only a vertically up-down motion and he will catch the ball when it comes back to the ground if the car has a constant velocity.
APPEARS IN
संबंधित प्रश्न
A bullet fired at an angle of 30° with the horizontal hits the ground 3.0 km away. By adjusting its angle of projection, can one hope to hit a target 5.0 km away? Assume the muzzle speed to the fixed, and neglect air resistance.
A cricket ball thrown across a field is at heights h1 and h2 from the point of projection at times t1 and t2 respectively after the throw. The ball is caught by a fielder at the same height as that of projection. The time of flight of the ball in this journey is
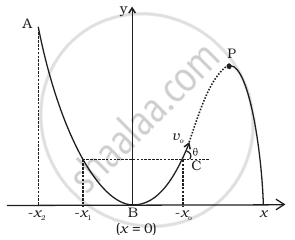
A particle slides down a frictionless parabolic (y = x2) track (A – B – C) starting from rest at point A (Figure). Point B is at the vertex of parabola and point C is at a height less than that of point A. After C, the particle moves freely in air as a projectile. If the particle reaches highest point at P, then
A boy throws a ball in air at 60° to the horizontal along a road with a speed of 10 m/s (36 km/h). Another boy sitting in a passing by car observes the ball. Sketch the motion of the ball as observed by the boy in the car, if car has a speed of (18 km/h). Give explanation to support your diagram.
A particle is projected in air at an angle β to a surface which itself is inclined at an angle α to the horizontal (Figure).
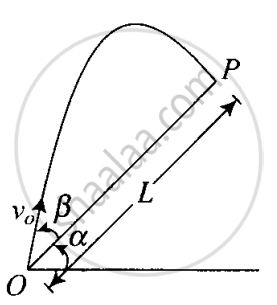
- Find an expression of range on the plane surface (distance on the plane from the point of projection at which particle will hit the surface).
- Time of flight.
- β at which range will be maximum.
A cricket fielder can throw the cricket ball with a speed vo. If he throws the ball while running with speed u at an angle θ to the horizontal, find
- the effective angle to the horizontal at which the ball is projected in air as seen by a spectator.
- what will be time of flight?
- what is the distance (horizontal range) from the point of projection at which the ball will land?
- find θ at which he should throw the ball that would maximise the horizontal range as found in (iii).
- how does θ for maximum range change if u > vo, u = vo, u < vo?
- how does θ in (v) compare with that for u = 0 (i.e.45)?
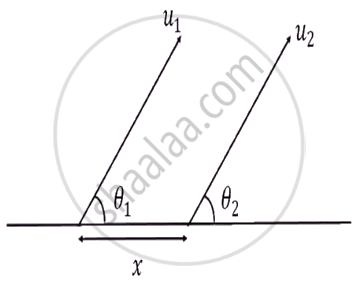
Two particles are projected simultaneously from the level ground as shown in figure. They may collide after a time:
If a baseball player can throw a ball at maximum distance = d over a ground, the maximum vertical height to which he can throw it, will be (Ball has same initial speed in each case):
The minimum speed in m/s with which a projectile must be thrown from origin at ground so that it is able to pass through a point P (30 m, 40 m) is ______. (g = 10 m/s2)
A ball is projected from the ground with a speed 15 ms-1 at an angle θ with horizontal so that its range and maximum height are equal, then tan θ will be equal to ______.
